Equações que Aprendem:
Uma Introdução aos Fundamentos Matemáticos da Aprendizagem Artificial
A. P. Rodrigues
___________________________________________________________________
Dados Internacionais de Catalogação na Publicação (CIP)
(Câmara Brasileira do Livro, SP, Brasil)
Rodrigues, A. P.
Equações que aprendem : uma introdução
aos fundamentos matemáticos da aprendizagem
artificial / A. P. Rodrigues. -- 1. ed. --
Passo de Torres, SC : Ed. do Autor, 2025.
ISBN 978-65-01-49720-4
1. Aprendizagem de máquina 2. Ciência da
computação 3. Inteligência artificial 4. Modelos
matemáticos 5. Redes neurais (Ciência da computação)
I. Título.
25-275449 CDD-006.3
Índices para catálogo sistemático:
1. Inteligência artificial 006.3
___________________________________________________________________
Dedico este livro…
Ao Eduardo, cuja gentil indicação bibliográfica me trouxe às redes neurais artificiais.
Ao professor Giovane pela disposição e atenção cálidas, e ao seu irmão, Vinícius.
Ao Daniel pelo papo, dicas e conselhos de valor inestimável.
Ao meu amigo querido, paizão mesmo, Marcus Maia.
Ao Fabiano e à Laura pela gratidão que virou tamanha generosidade.
À professora Carmen Mandarino.
Àquele que criou o neurônio sob cuja inspiração o Perceptron foi inventado.
Prefácio
Este é um e-book de distribuição gratuita, mas se você quiser, poderá adquirir uma cópia física no website do autor. Este livro é sobre a aprendizagem artificial e como este dom é dado a uma das estruturas mais fundamentais de todas as redes neurais: o Perceptron.
Este livro apresenta o que há de mais básico sobre a aprendizagem artificial em redes neurais. Qualquer pessoa pode utilizá-lo para ter um primeiro contato com o fascinante mundo em que as máquinas são capazes de aprender quase qualquer coisa e simular aspectos importantes da inteligência humana, como ver, ler, falar, entender o que outro ser humano fala, e várias outras capacidades utilíssimas e que têm estado cada vez mais ao alcance de todos.
Os dois primeiros capítulos deste livro costumavam compor um outro livro que eu havia intitulado de "O Mais Básico do Básico do Básico sobre a Aprendizagem Artificial". A presente obra é uma formidável ampliação da anterior. Embora o tratamento e o alcance do conteúdo do presente volume possam ser ditos ainda serem bem básicos, ele vai mais a fundo na aprendizagem das máquinas e mostra como dotar modelos profundos com a capacidade de aprender.
A aprendizagem artificial é o admirável segredo que está por trás das maravilhas que vemos, hoje em dia, nas IA’s mais conhecidas, como, por exemplo, o ChatGPT ou o Gemini. Sem ela, estes verdadeiros subprodutos monumentais da tecnologia não teriam sido possíveis. Para se construir uma inteligência artificial não basta apenas saber escrever código em alguma boa linguagem de programação como Tensorflow ou Pytorch. Estas mesmas linguagens são resultado de se haver dominado o entendimento de como fazer uma máquina, um software ou uma equação apreenderem e manterem o que gostaríamos de ensinar a elas.
No entanto, a aprendizagem está normalmente encapsulada em métodos, funções, classes, etc, daquelas linguagens e um excelente programador nunca precisa entrar em contato com elas, se não o desejar, para descrever em código a estrutura que deseja construir. Deste modo, o dom mais precioso de toda a inteligência artificial, em minha opinião, fica como que escondido.
O ocultamento, que é em parte um efeito colateral da automatização das camadas programáticas responsáveis pela aprendizagem, não é sem motivo. Ela amplia grandemente o número de pessoas que são capazes de dar vida a uma ideia através de inteligência artificial, mesmo sem jamais ter conhecido nada a respeito de como a aprendizagem artificial funciona.
Infelizmente, a matemática que descreve o fenômeno da aprendizagem não é normalmente ensinada antes do nível superior de educação no Brasil. E, embora ela não seja difícil e possa mesmo ser considerada conhecimento matemático antigo, o Cálculo Diferencial e a derivada de funções, acaba ficando desconhecido para um grande número de pessoas.
Este livro inteiro é sobre derivar funções! As funções em questão são os Perceptrons! Mas, os perceptrons são funções de um tipo um tanto mais elaborado. Não são funções reais. Eles são funções que envolvem matrizes e vetores!
O aprendizado artificial, que se baseia em derivadas, está baseado em uma técnica conhecida como "Propagar para trás" (back propagation, em inglês). Ela é o jeito certo de derivar uma função de tipo vetorial que seja compositivamente profunda. Este livro é sobre isto. Este é o principal conteúdo deste livro.
O que apresento nesta obra não é a única coisa que você deverá saber de importante sobre o aprendizado de máquina, mas é o indispensável! Sem este cerne central, o aprendizado artificial e as peças de inteligência artificial mencionadas acima não existiriam.
Escrevi este livro muito como eu mesmo gostaria de ter lido sobre o assunto quando comecei a estuda-lo. Tentei mostrar o que é, em minha opinião, o mais importante dentro do conjunto das coisas mais importantes, mostrando, por exemplo, as equações da estrutura do Perceptron e as do funcionamento da aprendizagem, de modo explícito e direto-ao-ponto, a fim de que qualquer um saiba exatamente como codificá-las, na sua linguagem preferida, tão logo lance um olhar sobre elas. Era isto o que eu gostaria ter encontrado quando comecei a estudar o assunto. Um tratamento elementar, acessível a principiantes, unitemático relativamente à aprendizagem e que fosse desde a conceituação, passando pela descrição detalhada e indo até a aplicação. Este livro, como já mencionado, enfoca fortemente a etapa descritiva.
No apêndice Tópicos Fundamentais em Aprendizado de Redes Neurais Não Tratados Neste Livro, você poderá encontrar uma lista de tópicos importantes em aprendizagem de máquina que não foram tratados, ou que tenham sido apenas mencionados, ou insuficientemente abordados na presente versão deste livro. Ela serve como uma boa referência temática inicial para aqueles que desejarão continuar alargando o seu conhecimento sobre o assunto.
Por fim, há alguns códigos que escrevi para este livro e que disponibilizei no notebook que está no repositório do GitHub. É bem possível que no futuro mais material ainda seja push(ado) para lá.
Tenha uma boa leitura!
- Prefácio
- Introdução
- 1. Vamos iniciar com uma brincadeira?
- 2. A Descrição Básica
- 3. O Aprendizado Artificial
- 3.1. Otimização
- 3.2. A Função de Custo
- 3.3. Gradiente do Erro com Relação a W
- 3.4. Gradiente do Erro com Relação ao bias b
- 3.5. Algumas Funções de Custo e de Ativação e suas Derivadas
- 3.6. Atualizando os Parâmetros Treináveis
- 3.7. Dando Vida às Equações
- 3.7.1. Aprendizagem Artificial: um primeiro exemplo.
- 3.7.2. Passo 2: Definindo as Ferramentas (Funções)
- 3.7.3. Passo 3: O Treino "à Mão" (Exemplo por Exemplo)
- 3.7.4. Passo 4: Analisando os Resultados do Treino
- 3.7.5. Passo 5: Testando o Modelo na Prática
- 3.7.6. Aprendizado Real sobre o Aprendizado Artificial
- 4. Múltiplas Camadas
- 4.1. A Propagação de um Sinal x Através das Camadas da Rede
- 4.2. Um Perceptron de 2 Camadas
- 4.2.1. A Equação de um Perceptron de 2 Camadas
- 4.2.2. A Função de Erro de Um Perceptron de 2 Camadas
- 4.2.3. As Taxas de Variação do Erro
- 4.2.4. Derivada do Erro com Relação aos Pesos da Camada 2
- 4.2.5. Derivada do Erro com Relação aos Bias da Camada 2
- 4.2.6. Derivada do Erro com Relação aos Pesos da Camada 1
- 4.2.7. Derivada do Erro com Relação aos Bias da Camada 1
- 4.3. Um Perceptron de Múltiplas Camadas
- 4.4. A Função de Erro de um Perceptron de Múltiplas Camadas
- 4.5. A Derivada do Erro com Relação aos Pesos de uma Camada Qualquer
- 4.6. Processo Prático Para a Atualização dos Pesos e Bias
- 4.7. Analisando a Dimensão das Matrizes de \( \frac{\partial E}{\partial W^l}\) e de \( \frac{\partial E}{\partial b^l}\)
- 4.8. A Atualização dos Pesos e Bias
- 4.9. Dando Vida às Equações
- 5. Treino em Lotes
- Apêndice A: Norma Sobre Um Espaço Vetorial
- Apêndice B: As Derivadas de \( y_i\)
- Apêndice C: Derivada de Funções Vetoriais
- Apêndice D: Algumas Observações sobre o Gradiente
- Apêndice E: Produto Externo
- Apêndice F: Aprendizado Contínuo
- Apêndice G: A Função de Custo sobre um Domínio Matricial é uma Norma
- Apêndice H: Tópicos Fundamentais em Aprendizado de Redes Neurais Não Tratados Neste Livro
- H.1. Inicialização de Pesos
- H.2. Normalização de Dados
- H.3. Taxa de Aprendizado e Otimizadores
- H.4. Regularização
- H.5. Arquiteturas de Rede
- H.6. Engenharia de Dados e Pré-processamento
- H.7. Técnicas de Treinamento
- H.8. Curvas de Aprendizado e Avaliação
- H.9. Transferência de Aprendizado (Transfer Learning)
Introdução
O Perceptron é, provavelmente, a mais básica de todas as arquiteturas de redes neurais. Embora possa ser utilizada sozinha em pequenos projetos e para pequenas tarefas, está presente, de um modo ou de outro, na grande maioria das peças de inteligência artificial mais conhecidas e badaladas atualmente, tais como o ChatGPT da OpenAI, ou o Transformer da Google.
Apresento a estrutura matemática mais básica do Perceptron, do seu funcionamento e, principalmente, do seu aprendizado, de forma rápida e direta-ao-ponto. O que abordo de teoria, aqui, é apenas o indispensável à apresentação, sem rodeios, desta peça fundamental da inteligência artificial atualmente. Assim, este livro não aborda a história do Perceptron, nem dá qualquer tratamento estatístico ou analítico geral aos objetos apresentados, nem aborda a teoria de matrizes ou conceitos de Álgebra Linear explicitamente, etc.
Algumas poucas demonstrações são feitas nos Apêndices, para o leitor interessado, mas só porque elas ajudam a esclarecer pontos importantes e basilares daquilo que este autor acredita ser o mais importante deste assunto inteiro: como é possível a uma rede neural aprender.
Assim, este livro foi escrito mais para exibir e operar com as fórmulas básicas, que trazem o entendimento primário e sólido do assunto, do que para prová-las ou demonstrá-las rigorosamente. Minha intenção primeira é apresentar e descrever, com boa clareza, aquilo que é o mais básico, matematicamente falando, a fim de que este primeiro contato dirija o leitor interessado a uma compreensão firme sobre o assunto e útil como base para leituras complementares ou mais avançadas, posteriormente.
As redes neurais e o Perceptron, em particular, são invenções humanas que foram baseadas no que se entendia sobre o funcionamento do neurônio. É um modelo que espelha longinquamente o funcionamento de um objeto natural vivo. Por mais distante que esteja o modelo do Perceptron daquilo que se conhece sobre a altíssima complexidade de um neurônio real, este modelo, não obstante, é de um sucesso grandioso.
Sendo uma invenção humana, a sua modelagem matemática mais fundamental é elegante e bela na medida mesma em que é demasiadamente simplista. O leitor provavelmente terá esta impressão em várias partes do livro, principalmente no primeiro capítulo e naquelas partes que tratam especificante da sua estrutura.
O conteúdo apresentado neste livro, principalmente, o que é exposto a partir do capítulo 2, foi criado com a intenção de colocar o leitor em condições de utilizar ou adequar facilmente os mesmos conceitos para o estudo de outras arquiteturas de redes neurais e de deep learning.
As modernas linguagens e frameworks tais como Tensorflow, baseiam-se e exploram o conceito de vetores e matrizes. Talvez, um dos méritos deste livro seja o de mostrar, explicitamente, a natureza matricial das equações que descrevem o Perceptron e, principalmente, daquelas que descrevem o seu aprendizado.
Por experiência, sabemos que para se construir redes neurais utilizando-se de ferramentas como o Tensorflow, não é imprescindível a um programador ter o conhecimento mais em profundidade que apresento aqui, pela simples razão de que ele está embutido como peça chave e, de certo modo, escondido debaixo de uma interface de altíssimo nível, intuitiva e simples de usar. Mas, a adequada, explícita e clara representação da natureza diferencial e matricial subjacente à aprendizagem artificial dará ao leitor a compreensão exata da beleza e do poder normalmente ocultos ao grande público maravilhado com os resultados luminosos advindos da aplicação de tais conhecimentos.
1. Vamos iniciar com uma brincadeira?
Vamos começar este livro com uma brincadeira!
Uma que você vai lembrar pelo resto da leitura deste livro. Talvez, pelo resto da vida.
Vamos "transformar" uma sequência de números no número \( \pi=3.14\). Isto mesmo que você leu: vamos transformar!
"Mas qual sequência de números?", você poderia perguntar. Qualquer uma serve, eu responderia! Você escolhe a sua!
A minha, vai ser a 1, 2, 3, 4!
Mas, eu poderia ter escolhido qualquer outra, como 3, 2, 1, 0, -1, -2; ou \(\frac{1}{2}, \frac{3}{4}, 100, -\frac{1256}{100}, 8^3, 0.67,\sqrt{\frac{1}{6}}\), não importando quais números estão na sequência ou quantos!
Mas, vamos precisar de uma outra sequencia de números! A que vai aprender a transformar [1, 2, 3, 4] no número único 3.14! Sim, precisamos de uma outra sequência! E, esta segunda sequencia é a sequencia mais importante.
Esta outra também pode começar com quaisquer números, mas ajuda muito se ela tiver, inicialmente, apenas números pequenos próximos de zero! E, esta outra sequência deve ter o mesmo número de elementos que a primeira.
Eu escolhi a seguinte: [0.9, 1.5, -0.1, 0.3].
Não há como frisar demais a importância desta sequência! Ela guardará o aprendizado responsável por transformar [1, 2, 3, 4] em 3.14.
Os quatro valores iniciais, que vemos no vetor de aprendizado, ainda não são tão importantes, mas os quatro valores que obtivermos, no fim, quando acabarmos de brincar, eles sim, são os mais importantes!
Pra começar, vamos combinar [1, 2, 3, 4] com [0.9, 1.5, -0.1, 0.3]! Isto mesmo! Vamos combinar! E, combinar linearmente! Ou seja, nós vamos encarar estas sequências como se fossem vetores e vamos multiplicar um vetor pelo outro, e ver no que dá:
Agora, 4.8 ainda não é 3.14 e nem próximo o bastante de 3.14!
Então, temos que fazer algo a respeito!
A versão inicial da nossa sequência de aprendizado tem um número negativo. Ele pode ser visto na primeira linha de 1. E se mexêssemos neste número de modo a obtermos, no final, um valor menor que 4.8 e mais próximo de 3.14?!?
O que poderíamos fazer com -0.1 de modo a transformar os 4.8 em um valor mais próximo de 3.14?
Veja que para se chegar em 3.14, a partir de 4.8, poderíamos fazer 4.8 - 1.66! Mas como mexer nos valores do vetor [0.9, 1.5, -0.1, 0.3] de modo a obtermos a diferença, -1.66, que precisamos, no valor final?
Vamos "chutar", como se diz, e se não der certo ainda, nós ajustamos mais tarde!
Então, vamos fazer o seguinte: vamos alterar -0.1 para -0.3; e vamos alterar também o 1.5 para 0.97.
Assim, nosso vetor de aprendizado inicial já está aprendendo (ou tentando!), pois ele foi de [0.9, 1.5, -0.1, 0.3] para [0.9, 0.97, -0.3, 0.3]!
E, vejam só!
Veja que alteramos apenas dois dos quatro números em nosso vetor inicial de aprendizagem. Mas, poderíamos ter alterado a todos!
O que exatamente fizemos àqueles dois valores do vetor original? Nós subtraímos 0.53 do 1.5 para obtermos 0.97 na segunda posição, e somamos -0.2 ao -0.1 para obtermos -0.3 na terceira posição. Achei o -0.53 e o -0.2 em repetidas tentativas. Observei o efeito que cada tentativa tinha em aproximar ou distanciar do resultado desejado, até encontrar valores cada vez mais próximos de 3.14!
Neste pequeno exemplo, acabamos de usar nossas inteligências reais para fazer algo parecido com o que modelos de inteligência artificial fazem corriqueiramente quando estão aprendendo!
Elas fazem pequenos ajustes em uma multidão de números distribuídos em muitos vetores. Estes vetores são, normalmente, muito grandes e os ajustes são feitos muitas e muitas vezes de modo que, a cada vez, as pequenas mudanças contribuam para levar o modelo inteiro a uma resposta mais próxima da resposta que se deseja que o modelo produza.
Este livro é sobre o modo belo, engenhoso e preciso em que estes tais ajustes são calculados e aplicados!
Veja que poderíamos ter feito ajustes em vários vetores ao mesmo tempo, cada um produzindo um resultado próprio! As nossas inteligências naturais achariam cansativo lidar com números em vários vetores a um nível de detalhe ínfimo e enfadonho! Mas, é exatamente o que os modelos de inteligência artificial podem fazer por nós!
Na verdade, estes modelos, também chamados de redes neurais artificiais, fazem muito mais do que só aproximar números. Eles são capazes de aproximar curvas e superfícies e, de um modo geral, eles podem aproximar ou mapear conjuntos de dados de natureza complicada e que descrevem, entre outras coisas, características da inteligência humana, como visão, audição ou fala.
Mencionei o conceito de mapeamento acima. Em nossa brincadeira, nós criamos um mapeamento! Um muito simples, mas, ainda assim, funcional. O mapeamento que criamos, usa o aprendizado que armazenamos no vetor [0.9, 0.97, -0.3, 0.3] para criar uma relação funcional entre um vetor, o [1,2,3,4] e o número 3.14, de modo que podemos simbolizar esta relação funcional, y=f(x), assim: \( f(x)=[0.9, 0.97, -0.3, 0.3] \cdot x\), de modo que \( f([1,2,3,4])=[0.9, 0.97, -0.3, 0.3] \cdot [1,2,3,4]=3.14\)!
Prepare-se, pois no restante do livro veremos muito mais sobre estes mapeamentos fabulosos e sobre como aplicar neles processos de otimização matemática automáticos que tornarão o aprendizado artificial uma verdadeira brincadeira de crianças.
1.1. Dando Vida às Equações
1.1.1. A Brincadeira Inicial em Código
Para começar a nos familiarizarmos com a implementação das ideias, vamos replicar a "brincadeira" da nossa Introdução usando Python e a biblioteca NumPy.
O código abaixo declara os dois vetores que usamos: o vetor de entrada x (os dados que queremos transformar) e o vetor de pesos w (o "conhecimento" da nossa equação). Veremos o resultado da combinação linear inicial, o "salto de aprendizado" com os pesos já ajustados, e a formalização da nossa relação funcional em um método f(x).
Cada linha de código espelha um passo da nossa brincadeira.
1import numpy as np
2
3# --- 1. O Ponto de Partida ---
4
5# O vetor de entrada que queremos "transformar".
6x = np.array([1, 2, 3, 4])
7
8# O vetor de pesos inicial, nosso "conhecimento" ainda incorreto.
9# No livro, chamamos esta de "sequência de aprendizado".
10w_inicial = np.array([0.9, 1.5, -0.1, 0.3])
11
12# A combinação linear (produto escalar) que fizemos no papel.
13resultado_inicial = np.dot(x, w_inicial)
14
15print(f"Vetor de Entrada (x): {x}")
16print(f"Pesos Iniciais (w_inicial): {w_inicial}")
17print(f"Resultado Inicial (x . w_inicial): {resultado_inicial:.2f}")
18print("---")
19
20
21# --- 2. O "Salto" de Aprendizado ---
22
23# Os pesos após o nosso ajuste "mágico", como fizemos na brincadeira.
24# Este é o "conhecimento" final que a equação aprendeu.
25w_final = np.array([0.9, 0.97, -0.3, 0.3])
26
27# A nova combinação com os pesos que "aprenderam" a tarefa.
28resultado_final = np.dot(x, w_final)
29
30print(f"Pesos Finais (w_final): {w_final}")
31print(f"Resultado Final (x . w_final): {resultado_final:.2f}")
32print("---")
33
34
35# --- 3. Formalizando o Aprendizado ---
36
37# Criamos uma função f(x) que encapsula o conhecimento aprendido.
38# Esta função é o nosso "modelo" final, pronto para ser usado.
39def f(vetor_entrada):
40 # Os pesos aprendidos estão "armazenados" dentro da função.
41 pesos_aprendidos = np.array([0.9, 0.97, -0.3, 0.3])
42 return np.dot(vetor_entrada, pesos_aprendidos)
43
44# Usando a função para provar que a transformação funciona.
45pi_calculado = f(x)
46
47print(f"Executando a função aprendida f(x):")
48print(f"f({x}) = {pi_calculado:.2f}")
49
50if np.isclose(pi_calculado, 3.14):
51 print("\nSucesso! A nossa equação aprendeu a calcular π!")1.1.2. A Brincadeira Ampliada: Ajuste Simultâneo
Agora, vamos estender a brincadeira. E se quiséssemos que um único conjunto de "neurônios" aprendesse a realizar várias tarefas ao mesmo tempo?
No exemplo abaixo, usaremos a mesma lógica, mas com uma matriz de pesos W. Cada linha da matriz W atuará como um "neurônio" separado, responsável por uma transformação diferente. Nosso objetivo é ajustar as três linhas de W para que, a partir de um único vetor de entrada x, nosso modelo calcule simultaneamente aproximações para três constantes famosas:
-
π (Pi) ≈ 3.14
-
e (Número de Euler) ≈ 2.71
-
h (Constante de Planck, valor escalado) ≈ 6.63
O fluxo é o mesmo: mostraremos o resultado com os pesos iniciais (aleatórios) e, em seguida, o resultado com os pesos finais "misteriosamente" ajustados, mostrando o poder de um ajuste simultâneo.
1import numpy as np
2
3# --- 1. Definição dos Alvos e da Entrada ---
4
5# Nossos alvos: as três constantes que queremos que a rede aprenda a gerar.
6# Nota: O valor de h (6.626e-34) foi escalado para 6.63 para fins didáticos.
7alvos = np.array([3.14, 2.71, 6.63]).reshape(3, 1) # Vetor coluna de respostas desejadas 'z'
8
9# Usaremos o mesmo vetor de entrada 'x' para todas as tarefas.
10x = np.array([1, 2, 3, 4]).reshape(4, 1) # Vetor coluna de entrada
11
12# --- 2. O Ponto de Partida com Pesos Aleatórios ---
13
14# A matriz de pesos inicial W. Cada linha é um "neurônio" com 4 pesos.
15# 3 neurônios (um para cada constante), 4 pesos cada. Forma da matriz: (3, 4).
16np.random.seed(42) # Para resultados reprodutíveis
17W_inicial = np.random.randn(3, 4) * 0.5 # Números aleatórios pequenos
18
19# A combinação linear inicial usando multiplicação de matrizes (W . x)
20# O resultado é um vetor de 3 elementos, um por neurônio.
21resultado_inicial = np.dot(W_inicial, x)
22
23print("--- Estado Inicial ---")
24print(f"Vetor de Entrada x:\n{x.T}")
25print(f"\nMatriz de Pesos Inicial W_inicial:\n{W_inicial}")
26print(f"\nResultado Inicial (W_inicial . x):\n{resultado_inicial}")
27print("Como esperado, o resultado inicial é aleatório e não se parece com nossos alvos.")
28print("-" * 25)
29
30
31# --- 3. O "Salto" de Aprendizado Simultâneo ---
32
33# Aqui está a matriz de pesos "mágica" após o ajuste.
34# Cada linha foi ajustada para sua respectiva tarefa.
35# (Estes valores foram pré-calculados para que o resultado seja o correto)
36W_final = np.array([
37 [0.9, 0.97, -0.3, 0.3], # Linha que "aprendeu" a calcular Pi
38 [0.1, 0.5, 0.8, -0.1525], # Linha que "aprendeu" a calcular 'e'
39 [1.0, 2.0, 0.9, -0.2425] # Linha que "aprendeu" a calcular 'h'
40])
41
42# A nova combinação com a matriz de pesos que "aprendeu" as três tarefas.
43# Veja, abaixo, que os resultados finais são muito próximos dos alvos desejados. Embora, pudéssemos ter obtido os valores exatos para π ≈ 3.14, e ≈ 2.71, e h ≈ 6.63, pela manipulação adequada dos dos pesos de W_final, em mais etapas de ajustes, isto é o que normalmente se obtém, numericamente, em projetos reais: aproximações muito boas.
44resultado_final = np.dot(W_final, x)
45
46print("\n--- Estado Final (Após o Aprendizado) ---")
47print(f"Matriz de Pesos Final W_final:\n{W_final}")
48print(f"\nResultado Final (W_final . x):\n{resultado_final}")
49print(f"\nAlvos Desejados:\n{alvos}")
50
51# Verificação do sucesso
52if np.allclose(resultado_final, alvos, atol=0.01):
53 print("\nSucesso! Nossa matriz de pesos aprendeu a realizar três tarefas simultaneamente!")2. A Descrição Básica
Entre as redes neurais artificiais, o perceptron é a mais simples.
O Perceptron é, digamos assim, o tijolo de construção da maioria dos modelos de redes neurais.
Sua estrutura é simples e fácil de entender.
Matematicamente, o Perceptron é uma equação que aprende.
Mas, o que a equação do Perceptron aprende? Qualquer coisa! Ela aprende a dar as respostas que desejemos que ela dê aos elementos de um conjunto qualquer de dados ou informações. Deste ponto de vista, o Perceptron aprende a criar um relacionamento matemático, ponto-a-ponto, entre um conjunto, \( D\), de dados e um outro conjunto, \( Z\), de respostas desejadas que assume a forma funcional \( P: D\longrightarrow Z\) e age como a equação \( P(d)=z\) entre pontos específicos.
2.1. Pesos e viéses ou Parâmetros Treináveis
Ele está baseado em uma matriz, \( W\), de parâmetros treináveis e também num vetor, \( b\), de outros parâmetros treináveis.
e
Estes parâmetros são ditos treináveis, pois eles se alteram durante o treino do perceptron, acumulando misteriosamente o aprendizado da rede, até atingirem um valor ótimo, quando a rede está pronta para desempenhar a tarefa para a qual foi criada.
Os elementos da matriz \( W\) são os pesos do perceptron, enquanto que o vetor \( b\) é o bias ou, em português, o viés. Os elementos de \( b\) são os viéses de cada neurônio.
Para colocar de forma muito simples e direta, o número de linhas de \( W\) é o número de neurônios do Perceptron e o número de colunas é o número de pesos de cada neurônio. Todos os neurônios (da mesma camada) têm o mesmo número de pesos.
Me referi ao perceptron como tijolo de construção da maioria das redes neurais. As redes neurais são construídas com estruturas básicas, chamadas camadas, e o Perceptron é esta camada numa grande maioria das arquiteturas de rede. Além disto, o Perceptron, ele próprio, pode ter camadas como veremos no Capítulo 3.
Veja que se o Perceptron fosse constituído de um único neurônio, então, a matriz, \( W\), representando esta camada seria, de fato, um vetor-linha! Ou seja, \( W\) seria a matriz \( 1\times m\):
Só para dar um exemplo, por incrível que possa parecer, mesmo projetos de Deep Learning, com arquiteturas mais complexas e profundas, mas que realizem classificação binária, provavelmente, estão utilizando um Perceptron com uma única linha de pesos como sua última camada. Este seria o caso de uma rede cujo objetivo fosse ler radiografias ósseas e dizer se elas indicam fraturas ou não. Uma tal rede, bem desenvolvida, poderia ser treinada para identificar fissuras ou fraturas que fossem difíceis de constatar pelo olho humano.
2.2. A Forma Geral do Perceptron
Um perceptron, assim como qualquer outra rede neural, é criado para desempenhar uma tarefa. Ele deve aprender a desempenhar a sua tarefa. Ele deve produzir um resultado, \( z\), condizente com cada elemento, \( x\), ambos em um conjunto, \( D\), de dados ou informações. Dizemos que \( D\) é um conjunto de vetores ou de tensores e que o perceptron é treinado sobre este conjunto. Falaremos mais sobre \( D\) quando chegarmos à Seção O Treino.
Se \( x\in D\) é um dos vetores de treino, então, a resposta, \( y\), do perceptron a este vetor é
O vetor \( x\) é uma das entradas do perceptron e \( y\) é a saída correspondente.
Qualquer das expressões em (6) são, às vezes, chamadas, simplesmente, de linearidade do perceptron.
2.3. Duas Representações Alternativas
Abaixo, apresento, rapidamente, duas formas alternativas em que o Perceptron pode ser considerado. O leitor poderá encontrá-las em outros livros, e saber que elas existem poderá alargar a sua capacidade de manipular as ferramentas matemáticas que o descrevem e o modelam. Eu as coloco aqui, de passagem, mas neste livro não as utilizaremos.
2.3.1. A forma \(\large xW\) do Produto Matricial
Note o leitor que a primeira equação de 6 poderia ter sido escrita com o vetor \( x\) multiplicando a matrix \( W\) desde a esquerda, assim
caso em que o vetor \( x^T\) seria um vetor-linha, as colunas de \( W^T\) seriam os neurônios do Perceptron, enquanto que o número de linhas de \( W^T\) seria o número de pesos em cada nerônio.
2.3.2. Pesos e Bias em uma Mesma Matriz
Podemos embutir o vetor de bias, de cada camada, em sua respectiva matriz de pesos, de modo que ele será a última coluna destas matrizes. Esta possibilidade já está dada nas equações do Perceptron. Considere, por exemplo, a terceira equação em 6 e repare que ela pode ser reescrita da seguinte forma
com \( b_i=w_{i(m+1)}\) e com \( x_{m+1}=1\).
Agora, note que a segunda equação em 8 é o mesmo que
Deste modo, só precisaríamos embutir a unidade escalar como a última posição de cada vetor entrante, \( x\), de modo que agora ele passe a ter \( m+1\) elementos.
Deste modo, a equação acima é simplesmente
2.4. Funções de Ativação
É extremamente comum entregar cada um dos valores de \( y\) a uma mesma função de ativação. Esta função de ativação também é conhecida como "não-linearidade", por "quebrar", de algum modo, o comportamento linear que é produzido em 6. Ela pode assumir uma de várias formas comumente utilizadas. No momento, vamos apenas designá-las por um símbolo: \( a\). Assim, em sua forma mais geral, o perceptron de uma camada é
Esta última expressão pode parecer um pouco confusa, no momento, talvez por causa das expressões que estão dentro dos colchetes, mas não estranhe. Ela exibe os símbolos matemáticos que espelham a estrutura conceitual de um Perceptron de uma camada. Ela também mostra como o vetor \( x\) é "absorvido" e processado pela rede. Os vetores \( W_i\) são as linhas de \( W\) e os escalares \( b_i\) são elementos de \( b\). Veja como o vetor \( x\) é processado por cada uma das linhas de \( W\). A equação mostra como o sinal \( x\) "flui" através do perceptron até ser transformado na sua resposta, \( P\).
Procure fixar bem o fato de que \( a\) é um vetor e que seus elementos são funções cujas variáveis independentes são, respectivamente, os elementos do vetor \( y\). Na Subseção, abaixo, coloquei uma tabela com algumas funções de ativação bem conhecidas e utilizadas.
2.4.1. Algumas Funções de Ativação
A tabela, abaixo, exibe algumas das funções de ativação mais conhecidas. Elas são mostradas com a notação que utilizamos durante todo o livro, revelando a sua natureza de função real de domínio real, com exceção da Função Softmax. A função Softmax utiliza todas as componentes de um vetor de linearidades para gerar um percentual relativo à \( i\)-ésima componente.
| Nome | Fórmula |
|---|---|
Sigmoid |
\( a_i(y_i)=\frac{1}{1+e^{-y_i}}\) |
Tangente Hiperbólica |
\( a_i(y_i)=\tanh(y_i)\) |
Softmax |
\( a_i(y) = \frac{e^{y_i}}{\sum_{k=1}^{n}e^{y_k}}\) |
ReLU |
\( a_i(y_i) = \max\{0,y_i\}\) |

2.5. O Treino
Já dissemos que um perceptron deve aprender a realizar uma certa tarefa e que ele é treinado sobre um conjunto de dados ou informações, \( D\). Este conjunto pode ser considerado um conjunto de duplas ordenadas, \( (x,z)\in D\), de modo que \( z\in Z\subset D\) e \( x\in X\subset D\) são, respectivamente, o conjunto das respostas desejadas e o conjunto dos vetores que representem um domínio qualquer de coisas que nos interesse relacionar com as respostas desejadas.
Nós já vimos que \( x\) é um vetor. A segunda componente da dupla ordenada, \( (x,z)\), é a resposta que desejamos que o perceptron aprenda a dar ao vetor de entrada \( x\). A ordenada \( z\) pode ser um número escalar, um vetor, uma matriz, ou um tensor. Isto vai depender de como codificamos a tarefa, matematicamente. Neste livro, as nossas respostas desejadas, \( z\), serão apenas escalares ou vetores.
Inicialmente, o perceptron dá uma resposta qualquer, \( P\), ao vetor \( x\). Ao longo do treino, esta resposta vai se aproximando da resposta correta ou desejada, \( z\). Verificamos esta aproximação com uma Função de Custo, que indicaremos com o símbolo \( E\), (veremos mais sobre ela na Seção A Função de Custo), a qual nos diz quão longe ou quão perto \( P(x)\) está da resposta desejada \( z\). Ao longo do treino, o valor da Função de Custo vai diminuindo pois \( P(x)\) vai se tornando cada vez mais próxima de \( z\). O nosso objetivo durante um treino é fazer com que o erro vá para zero, ou seja, que a igualdade \( P(x)=z\) seja verdadeira, ou quase verdadeira, pois, normalmente um erro suficientemente pequeno já é o bastante.
Sob certo ponto de vista, este livro inteiro é sobre como reintegrar no Perceptron, durante o treino, a informação contida no erro, \( E\), de modo a fazer o Perceptron acertar cada vez mais em sua tarefa. Isto é, criar o relacionamento que desejamos, \( P(x_i)=z_i\), entre
Há várias funções que podem ser utilizadas como função de custo ou de perda. A escolha depende do projeto e, às vezes, do gosto de quem treine a rede. Na Seção Algumas Funções de Custo, há uma tabela com algumas funções de custo úteis e comumente utilizadas. O importante a saber é que a Função de Custo, seja ela qual for, deve cumprir com a definição matemática de norma, assunto no qual não entraremos neste livro, mas cuja definição pode ser encontrada pelo leitor interessado no Apêndice Norma Sobre Um Espaço Vetorial, junto com uma pequena demonstração de que se uma norma é nula, então o seu argumento também o é.
Veremos na Seção Atualizando os Parâmetros Treináveis que o processo que utilizaremos para aproximar \( P(x)\) e \( z\) baseia-se no gradiente da Função de Erro. Este processo, chamado de Descida do Gradiente ou Descida Estocástica do Gradiente, indica gradualmente a direção do menor valor de \( E\) e, deste modo, também indica o caminho de um menor valor de separação entre \( P\) e \( z\).
Podemos dizer que o Perceptron é um mapeamento que aprende a dar uma resposta \( z\) adequada a cada \( x\) num processo de aprendizado que é realizado durante uma ou várias sessões de treino. Normalmente, várias! Numa sessão de treino, o Perceptron recebe todos os elementos \( x\) de \( D\), um após o outro e, para cada \( x\), calcula-se o \( P(x)\) correspondente. Após isto, calcula-se a função de erro sobre \( P(x)\) e \( z\), de modo que podemos expressa-la assim: \( E(P,z)\). Realiza-se tantas sessões de treino quantas forem necessárias para fazer \( E(P,z)\) suficientemente próxima de zero. Esta é a razão para se exigir que a Função de Erro ou de Custo seja uma norma, pois aí, quando \( E(P,z)\longrightarrow 0\), também será verdade que \( P-z\longrightarrow 0\), ou seja, a resposta da rede estará se tornando igual à resposta desejada.
3. O Aprendizado Artificial
3.1. Otimização
O aprendizado artificial é um processo de otimização.
O que é otimizado no aprendizado artificial? Uma função que normalmente é chamada de Função de Custo ou de Perda, ou, ainda, Função de Erro! Eu, pessoalmente, a chamo, neste contexto de aprendizado artificial, de Função Pedagógica, uma vez que ela mede o quão distante está a resposta do Perceptron da resposta desejada e, por este meio, sabemos se a rede está aprendendo ou não. É a partir da derivação da Função de Perda que o aprendizado acontece.
Qualquer um que já tenha derivado uma função para, logo em seguida, encontrar o seu máximo ou o seu mínimo, está em perfeitas condições de saber como o aprendizado artificial acontece.
O aprendizado ocorre em uma ou mais sessões de treino, em que os parâmetros treináveis do Perceptron são repetidamente atualizados (Ver Seção O Treino). Estes parâmetros são atualizados a cada passo do treino, ou seja, depois que cada lote de treino é apresentado à rede. Veremos mais sobre o treino em lotes na Seção Treinando Em Lotes.
A descrição de como o aprendizado artificial acontece é a parte mais importante e interessante das redes neurais na opinião deste autor. Sem isto, não há aprendizado de máquina.
3.2. A Função de Custo
Quando vamos à escola, o nosso aprendizado é medido por avaliações. O aprendizado das redes neurais também é aferido por avaliações de desempenho.
A escola do Perceptron é a sessão de treino.
Assim como a nota escolar final é obtida a partir de uma fórmula, as redes neurais também se utilizam de fórmulas que “dão nota” ao seu desempenho.
No caso das redes neurais, tais fórmulas são conhecidas como funções de custo ou de perda ou, ainda, de erro. Neste livro, me refiro a elas muito mais como funções de erro. Elas, de fato, medem o erro cometido pela rede ao tentar prever uma resposta a uma entrada correspondente.
A função de erro pode ter várias formas, mas não abordarei nenhuma forma específica agora, pois estamos interessados no encaixe que a sua forma geral tem nas fórmulas do aprendizado. Neste momento, vamos apenas simbolizar uma função de erro qualquer com a letra \( E\). Na Subseção Algumas Funções de Custo, logo abaixo, é possível encontrar uma tabela com algumas funções de custo.
Há muito o que dizer sobre \( E\) mas, por ora, vamos nos ater aos aspectos operacionais que tornam possível ao perceptron aprender.
A função \( E\) toma como argumento a saída do Perceptron. Então,
Ma, veja, a saída do perceptron depende dos seus parâmetros treináveis, ou seja, \( E\) também depende dos pesos e bias. Então, é mais comum escrevermos
Esta notação é muito útil, pois o aprendizado do perceptron depende da derivada de \( E\) com relação aos seus pesos e bias.
Aqui, precisamos considerar a estrutura compositiva da função de erro,
e, manter em mente que \( a\) e \( y\) são vetores, os dados em 6 e 11, e que \( E\) é uma função real.
3.2.1. Algumas Funções de Custo
Abaixo, estão algumas das Funções de Custo (de domínio vetorial) mais conhecidas.
| Nome | Fórmula |
|---|---|
Erro Quadrado Médio |
\( E=\frac{1}{n}\sum_{i=1}^n(a_i-z_i)^2\) |
Erro Médio Absoluto |
\( E=\frac{1}{n}\sum_{i=1}^n \begin{vmatrix}a_i-z_i\end{vmatrix}\) |
Entropia Cruzada |
\( E=-\frac{1}{n}\sum_{i=1}^n z_i\cdot \log a_i\) |
Entropia Cruzada Binária |
\( E=-\frac{1}{n}\sum_{i=1}^n \begin{bmatrix}z_i\cdot \log a_i+(1-z_i)\cdot \log (1-a_i)\end{bmatrix}\) |
3.3. Gradiente do Erro com Relação a W
Vamos calcular a derivada da função de erro com relação aos pesos do Perceptron. Esta derivada também é conhecida como o gradiente do Erro.
Sabemos que \(\frac{\partial E}{\partial a}\) é o gradiente de \( E\) com relação ao vetor de ativações \( a\), pois \( E\) é uma função real com domínio vetorial. Assim, \(\frac{\partial E}{\partial a}=\nabla_a E\).
A derivada \(\frac{\partial a}{\partial y}\) gera uma matriz. Isto vem do fato de que tanto \( a\) como \( y\) sejam funções vetoriais. Veja o apêndice Derivada de Funções Vetoriais para mais detalhes sobre derivadas de funções vetoriais.
Por esta razão, as derivadas \(\frac{da_i}{d y_i}\) ainda não podem ser calculadas ou completamente reduzidas. Isto acontecerá quando estivermos tratando de exemplos ou de arquiteturas específicas.
Se analisarmos a equação 11, veremos que cada \( a_i\) depende apenas de \( y_i\). Portanto, devemos ter \(\frac{d a_i}{d y_j}=0\) se \( i \ne j\). Portanto, \(\frac{\partial a}{\partial y}\) será uma matriz diagonal. Os elementos, \(\frac{da_i}{d y_i}\), desta matriz diagonal dependerão da forma específica de \( a\).
A diferencial \(\frac{\partial y}{\partial W}\) tem a forma de um vetor-coluna de \( n\) elementos. Só que estes elementos, por sua vez, são matrizes \( n\times m\).
Agora, veja que cada elemento, \( i\), do vetor-coluna que está no segundo membro de 16 é a derivada de uma função real cujos argumentos coincidem apenas com a linha \( i\) de \( W\). Estas funções reais estão definidas na equação 6, de onde sabemos que \( y_i(W_i)=\sum_{j=1}^{m} w_{ij}x_j +b_i\) (Veja o Apêndice As Derivadas de \( y_i\) para relembrar o procedimento de derivação desta equação). Portanto, os elementos do vetor-coluna são matrizes com entradas nulas, com a única exceção de sua linha \( i\).
Vetores-coluna ou vetores-linha de matrizes aparecerão muitas vezes nesta apresentação. Isto decorre do fato de estarmos derivando o erro, \( E\), com relação à matriz inteira, de pesos de uma só vez.
Deste modo, a fórmula 15, que calcula a derivada parcial do erro \( E\) do perceptron com relação aos seus pesos, \( W\), é
3.4. Gradiente do Erro com Relação ao bias b
Nós, agora, precisamos calcular a derivada de E com relação ao vetor de viéses, \( b\).
De 6, nós vemos que os viéses estão entranhados no nível mais profundo do perceptron, juntamente com os pesos.
Antes, consideramos o erro como função apenas dos pesos. Agora, vamos considerá-los como função apenas dos viéses ou bias.
Pelos cálculos que já fizemos na seção anterior, podemos muito simplesmente escrever.
Se necessário, veja o Apêndice As Derivadas de \( y_i\) para mais considerações sobre o cálculo de \(\frac{\partial y}{\partial b}\).
3.5. Algumas Funções de Custo e de Ativação e suas Derivadas
| Nome | Fórmula | Derivada \(\left(\frac{d a_i}{d y_i}\right)\) |
|---|---|---|
Sigmoid |
\( a_i(y_i)=\frac{1}{1+e^{-y_i}}\) |
\(\begin{aligned} &\frac{e^{-y_i}}{(1+e^{-y_i})^2}\\ &\text{ou}\\ &a_i(1-a_i) \end{aligned}\) |
Tangente Hiperbólica |
\( a_i(y_i)=\tanh(y_i)\) |
\(\begin{aligned} &1-tanh^2 y_i\\ &\text{ou}\\ &1-a_i^2 \end{aligned}\) |
Softmax |
\( a_i(y) = \frac{e^{y_i}}{\sum_{i=1}^{n}e^{y_i}}\) |
\(\begin{aligned} &\frac{e^{y_i}}{\sum_{j=1}^{n}e^{y_j}} \left( 1- \frac{e^{y_i}}{\sum_{j=1}^{n}e^{y_j}} \right )\\ &\text{ou}\\ &a_i(1-a_i) \end{aligned}\) |
ReLU |
\( a_i(y_i) = \max\{0,y_i\}\) |
\(\max\{0,1\}\) |
| Nome | Fórmula | Derivada \(\left(\frac{d E}{d a_i}\right)\) |
|---|---|---|
Erro Quadrado Médio |
\( E=\frac{1}{n}\sum_{i=1}^n(z_i-a_i)^2\) |
\( -\frac{2(z_i-a_i)}{n}\) |
Erro Médio Absoluto |
\( E=\frac{1}{n}\sum_{i=1}^n \begin{vmatrix}a_i-z_i\end{vmatrix}\) |
\(\begin{equation*} \begin{aligned} &\frac{1}{n} \frac{a_i-z_i}{\begin{vmatrix}a_i-z_i\end{vmatrix}}\\ &\text{ou}\\ &\frac{1}{n} \begin{cases} 1 & \text{se}\ \ a_i>z_i \\ -1 & \text{se}\ \ a_i<z_i \\ \nexists & \text{se }\ \ a_i=z_i \end{cases} \end{aligned} \end{equation*}\) |
Entropia Cruzada |
\( E=-\frac{1}{n}\sum_{i=1}^n z_i\cdot \log a_i\) |
\( -\frac{z_i}{na_i}\) |
Entropia Cruzada Binária |
\( E=-\frac{1}{n}\sum_{i=1}^n \begin{bmatrix}z_i\cdot \log a_i +(1-z_i)\cdot \log (1-a_i)\end{bmatrix}\) |
\(\frac{a_i-z_i}{a_i(1-a_i)}\) |
3.6. Atualizando os Parâmetros Treináveis
Por fim, chegamos aonde queríamos: \( \frac{\partial E}{\partial W}\) e \( \frac{\partial E}{\partial b}\) serão utilizados para atualizar os pesos e bias do perceptron. O processo em que isto é feito é chamado de retro-propagação e se baseia na técnica da Descida Estocástica do Gradiente. Esta técnica se baseia, por sua vez, no fato de que \( \frac{\partial E}{\partial W}\) é um vetor gradiente e que, portanto, sempre se orienta na direção da maior taxa de variação de \( E\). Portanto, o seu negativo, \( -\frac{\partial E}{\partial W}\), (ver nas fórmulas 21 e 23) apontará na direção da menor variação. Não entrarei em maiores detalhes sobre este ponto aqui, mas o leitor interessado poderá ler algumas outras poucas observações interessantes e pertinentes ao uso que fazemos, no Apêndice Algumas Observações sobre o Gradiente. Apenas adiantarei que o mencionado sinal negativo é muito importante. Se você já codificou esta fórmula, digamos em Python ou em Tensorflow ou qualquer outra linguagem ou framework, para treinar um Perceptron, mas, por engano, usou um sinal positivo no lugar do negativo, pode constatar que o erro cometido pelo Perceptron de fato só aumenta ao invés de diminuir!
No momento, já temos tudo o que é necessário à apresentação da fórmula que permite que o aprendizado aconteça. Esta fórmula tem tal simplicidade e beleza, que só é igualada por seu poder de tornar possível o aprendizado do Perceptron.
Durante uma sessão de treino, os pesos do Perceptron são atualizados muitas vezes. Cada atualização acontece em um momento, \( t\), do treino. À medida que o treino evolui, os pesos vão sendo alterados na busca de um melhor desempenho, ou seja, na busca de um custo, \( E\), menor. Em um dado momento, \( t\), do treino, o perceptron tem a matriz \( W_t\) de pesos que sofre a adição de \( \Delta W_t\) cujo resultado passa a ser a nova matriz atual de pesos do Perceptron, \( W_{t+1}\).
em que
O símbolo \( \eta\) é chamado de taxa de aprendizagem. É um parâmetro cuja importância está em ditar a cadência do treino, pois com ele é possível ajustar a “velocidade” do treino. No entanto, é difícil saber qual é a velocidade ótima para cada passo do treino de uma rede neural, embora haja orientações gerais e métodos úteis de cálculo, sobre os quais não falaremos neste momento. É um parâmetro de manejo algo delicado como, aliás, são também outros parâmetros definidores de redes neurais. Na prática, valores pequenos como \( \eta=0.01\) ou \( \eta=0.001\) são sempre utilizados como uma primeira alternativa. Outras abordagens alteram o valor de \( \eta\) ao longo do treino de modo que o seu valor vai diminuindo à medida em que o treino avança.
A atualização do bias é feita com fórmulas bem similares as da atualização dos pesos:
em que
3.7. Dando Vida às Equações
3.7.1. Aprendizagem Artificial: um primeiro exemplo.
Este notebook implementa nosso primeiro Perceptron funcional em sua forma mais simples possível: uma única camada com um único neurônio. Usaremos apenas Python e NumPy para ver a teoria dos Capítulos 1, 2 e 3 em sua forma mais pura.
O objetivo é aplicar a retropropagação (backpropagation) a um problema real e bastante rudimentar de classificação de imagens. Como nossa arquitetura é a mais simples que existe, veremos como a equação geral do aprendizado 17 se simplifica de uma maneira bela e intuitiva. O cálculo do gradiente dos pesos (∂E/∂W), por exemplo, não terá aquele desajeitado vetor-coluna de matrizes, como veremos.
1import numpy as np
2import matplotlib.pyplot as plt
3import requests
4from PIL import Image
5from io import BytesIO
6
7# Função para baixar e preparar uma imagem a partir de uma URL
8def download_and_prepare_image(url):
9 response = requests.get(url)
10 img = Image.open(BytesIO(response.content))
11 img = img.convert('L')
12 img_array = np.array(img) / 255.0
13 img_array = np.where(img_array > 0.7, 1, 0)
14 return img_array.flatten()
15
16# URLs das imagens de "carinhas"
17base_url = 'https://raw.githubusercontent.com/aleperrod/perceptron-book/2e9af4436dd7317ea18fbcae583429cccc944ef0/carinhas/'
18urls = [
19 base_url + 'gross1.png', base_url + 'gross2.png', base_url + 'gross3.png',
20 base_url + 'thin1.png', base_url + 'thin2.png', base_url + 'thin3.png'
21]
22
23X_train = np.array([download_and_prepare_image(url) for url in urls])
24z_train = np.array([0, 0, 0, 1, 1, 1])
25
26# Imagens de teste
27url_teste_thin = base_url + 'thin4.png'
28url_teste_gross = base_url + 'gross4.png'
29x_teste_thin = download_and_prepare_image(url_teste_thin)
30x_teste_gross = download_and_prepare_image(url_teste_gross)1# Visualizando nossos dados de treino
2fig, axes = plt.subplots(1, 6, figsize=(15, 3))
3for i, ax in enumerate(axes):
4 ax.imshow(X_train[i].reshape(20, 20), cmap='gray') # Erro no reshape, corrigido para 20x20
5 ax.set_title(f"Classe: {'Gross' if z_train[i] == 0 else 'Thin'}")
6 ax.axis('off')
7plt.suptitle("Amostra dos Dados de Treino ('Carinhas')", fontsize=16)
8plt.show()
3.7.2. Passo 2: Definindo as Ferramentas (Funções)
Como estamos construindo tudo "à mão", definimos nossas ferramentas como funções separadas. Note que, como nosso Perceptron tem um só neurônio, a saída P e o erro E são valores únicos (escalares), o que simplifica suas derivadas.
1# Funções de Ativação e suas derivadas
2def sigmoid(y):
3 return 1 / (1 + np.exp(-y))
4
5def sigmoid_derivative(a):
6 return a * (1 - a)
7
8# Função de Custo (Erro Quadrado Médio) e sua derivada
9# z e P são escalares aqui
10def mean_squared_error(z, P):
11 return (z - P)**2
12
13def mean_squared_error_derivative(z, P):
14 return 2 * (P - z) # Mantendo o fator 2 para fidelidade à derivada formal
15
16# Função para inicializar os parâmetros do nosso neurônio
17def inicializar_parametros(dim_entrada):
18 # W é um vetor 1D (não uma matriz) com 400 pesos.
19 W = np.random.randn(dim_entrada) * 0.01
20 # b é um único número (escalar)
21 b = 0.0
22 return W, b3.7.3. Passo 3: O Treino "à Mão" (Exemplo por Exemplo)
Este é o coração do nosso notebook. O loop de treino implementa a teoria do aprendizado artificial. Para cada imagem x e seu rótulo z, o processo é:
-
Propagação para Frente (Forward Pass): Calculamos a saída
P, que neste caso é um único número. -
Backpropagation: Calculamos os gradientes. Aqui está a beleza da simplificação:
-
O "delta" do erro
dE/dyé um escalar, já que há uma única linearidade,y. -
O gradiente dos pesos,
dE/dW, é calculado multiplicando este delta escalar pelo vetor de entradax. A equação∂E/∂W = (∂E/∂a * ∂a/∂y) * xse manifesta aqui. A expressão 17 se simplifica pois, neste exemplo, a matriz de pesos,Wreduz-se a um vetor-linha!
-
-
Atualização: Ajustamos
Webusando os gradientes calculados.
1# --- Hiperparâmetros e Inicialização ---
2taxa_aprendizagem = 0.1
3epocas = 30
4W, b = inicializar_parametros(X_train.shape[1])
5
6historico_custo = []
7
8print("Iniciando o treino em Python/NumPy (versão corrigida)...")
9for i in range(epocas):
10 custo_total_epoca = 0
11 # O loop interno itera sobre cada exemplo individualmente
12 for x, z in zip(X_train, z_train):
13
14 # --- 1. Forward Pass ---
15 # y = W . x + b (produto escalar entre dois vetores -> escalar)
16 y = np.dot(W, x) + b (1)
17 # P = a(y) (ativação sobre um escalar -> escalar)
18 P = sigmoid(y) (2)
19
20 # --- 2. Cálculo do Custo ---
21 custo = mean_squared_error(z, P)
22 custo_total_epoca += custo
23
24 # --- 3. Backpropagation (com escalares) ---
25 # Delta inicial: dE/dy = dE/dP * dP/dy (produto de escalares)
26 dE_dP = mean_squared_error_derivative(z, P)
27 dP_dy = sigmoid_derivative(P)
28 dE_dy = dE_dP * dP_dy
29
30 # Gradientes dos parâmetros
31 # dE/dW = dE/dy * d(y)/dW = dE/dy * x
32 # Esta é a forma simplificada! É a multiplicação de um escalar (dE_dy) por um vetor (x).
33 dE_dW = dE_dy * x
34 # dE/db = dE/dy * d(y)/db = dE/dy * 1
35 dE_db = dE_dy
36
37 # --- 4. Atualização dos Parâmetros ---
38 W -= taxa_aprendizagem * dE_dW
39 b -= taxa_aprendizagem * dE_db
40
41 # Fim da época
42 custo_medio = custo_total_epoca / len(X_train)
43 historico_custo.append(custo_medio)
44 if (i + 1) % 5 == 0:
45 print(f"Época {i + 1}/{epocas} - Custo Médio: {custo_medio.item():.6f}")
46
47print("Treino finalizado!")| 1 | Aqui, a linearidade \( y=W\cdot x+b\) que, para o nosso caso presente, é \( y=\begin{bmatrix}w_{1}&,\dots , & w_{400}\end{bmatrix}\cdot\begin{bmatrix} x_1 , \dots , x_{400}\end{bmatrix}^t+b\) (o sobrescrito \( t\) denota a transposição de linha para coluna) que, por sua vez, equivale a \( y=w_{1}x_1+\dots +w_{400}x_{400} +b\). |
| 2 | Retornamos a função de ativação sigmoid \( P=a(y)=\frac{1}{1+e^{-y}}=\frac{1}{1+e^{-(W\cdot x+b)}}=\frac{1}{1+e^{-(w_{1}x_1,\dots , w_{400}x_{400} +b)}}\). |
3.7.4. Passo 4: Analisando os Resultados do Treino
Uma coisa é executar o treino, outra é saber se ele funcionou. O gráfico abaixo mostra a evolução do custo médio ao longo das épocas.
Uma curva descendente é o sinal que procuramos: ela indica que o Perceptron estava, a cada passagem pelos dados, ajustando seus pesos e se tornando progressivamente melhor em sua tarefa, ou seja, o erro estava diminuindo.
1# Plotar o gráfico da função de custo para ver se a rede aprendeu
2plt.figure(figsize=(10, 6))
3plt.plot(historico_custo, marker='o', linestyle='-')
4plt.xlabel("Época")
5plt.ylabel("Erro / Custo Médio")
6plt.title("Evolução do Erro Durante o Treino (Python/NumPy)")
7plt.grid(True)
8plt.xticks(np.arange(len(historico_custo)), np.arange(1, len(historico_custo) + 1))
9plt.show()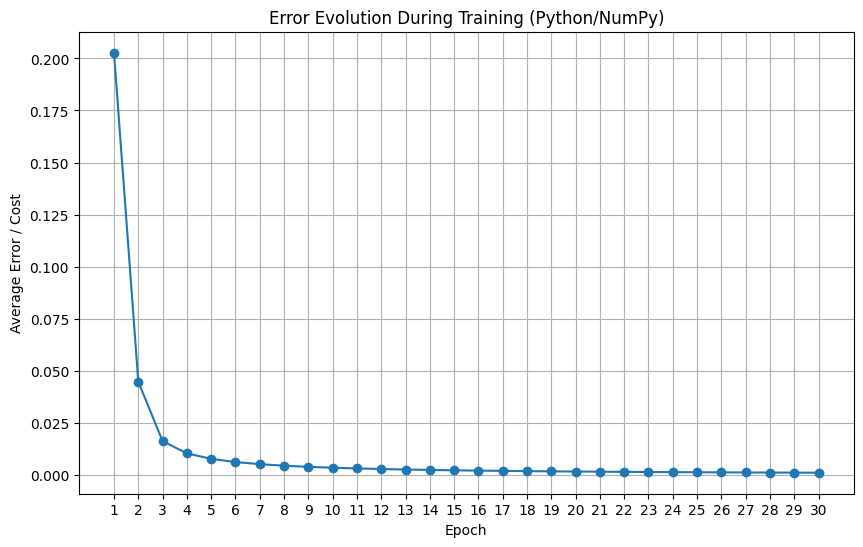
3.7.5. Passo 5: Testando o Modelo na Prática
Após o treinamento, o verdadeiro teste de uma rede neural é seu desempenho em dados que ela nunca viu antes. A célula abaixo define uma função que pega uma imagem de teste, aplica o forward pass com os pesos W e o bias b que acabamos de treinar, e exibe a imagem com a predição do modelo ao lado do rótulo real.
A saída da função Sigmoid (P) é um número entre 0 e 1. Podemos interpretá-lo como a "confiança" do neurônio de que a imagem pertence à classe "Thin" (rótulo 1). Usamos um limiar (threshold) de 0.5 para tomar a decisão final.
Execute a célula para ver se o Perceptron acerta!
1# Função para testar o modelo treinado em uma nova imagem
2def testar_modelo_numpy(imagem, label_real_str, W, b):
3 # O Forward Pass é o mesmo que dentro do loop de treino
4 y = np.dot(W, imagem) + b
5 P = sigmoid(y)
6
7 # A classificação é baseada em um limiar (threshold) de 0.5
8 predicao_final = "Thin" if P > 0.5 else "Gross"
9
10 # Exibindo os resultados
11 print(f"--- Testando a imagem: '{label_real_str}' ---")
12 print(f"Saída do neurônio (P): {P.item():.4f}")
13 print(f"Predição final: {predicao_final}")
14
15 plt.imshow(imagem.reshape(20, 20), cmap='gray')
16 plt.title(f"Predição: {predicao_final} | Real: {label_real_str}")
17 plt.axis('off')
18 plt.show()
19
20# Testando com as duas imagens que separamos
21print("Iniciando testes com dados não vistos...\n")
22testar_modelo_numpy(x_teste_thin, "Thin", W, b)
23print("\n" + "="*40 + "\n")
24testar_modelo_numpy(x_teste_gross, "Gross", W, b)3.7.6. Aprendizado Real sobre o Aprendizado Artificial
Nosso perceptron, com um único neurônio, aprendeu a distinguir imagens com forte predominância de preto de imagens com forte predominância de branco. As primeiras têm traços brancos sobre um fundo preto e as outras têm, ao contrário, traços em preto sobre um fundo branco. Mas, como, exatamente, ele fez isto?
Graças à simplicidade de uma rede neural artificial, "de brinquedo", composta de um único neurônio, podemos dar uma resposta bem enraizada, não só na arquitetura de tal rede, mas em seu funcionamento numérico.
O nosso perceptron é composto de uma única combinação linear, \( y=w_{1}x_1+\dots +w_{400}x_{400} +b\), cujo resultado, \( y\), é dado a uma função de ativação sigmoide.
Por um lado, os pesos \( W=[w_1, \dots , w_{400}]\) são inicializados, cada um, com valores pequenos, W = np.random.randn(dim_entrada) * 0.01.
O "pulo de gato", por outro lado, está em transformar nossas imagens em vetores de zeros e uns,img_array = np.where(img_array > 0.7, 1, 0), ou seja, para cada elemento de \( x=[x_1, \dots , x_{400}]\), temos \( x_i\in \{0,1\}\), sendo que para as imagens com fundo preto, predominam \( i's\) com \( x_i=0\), enquanto que, para as com fundo branco, predominam \( i's\) com \( x_i=1\).
Agora, precisamos ver que \( 0\le \sum_{i=0}^{400} x_i \le 400\), pois, no caso improvável em que todas as posições do vetor \( x\) fossem nulas, então, este somatório seria nulo, enquanto que, no caso, igualmente improvável, em que todas as posições fossem iguais à unidade, a soma seria 400!
Podemos inspecionar visualmente e verificar que as posições de \( W\), após o treino, se encontram dentro de um intervalo diminuto, contido no intervalo \( (-1, 1)\), ou seja, sendo um número pequeno, vale a desigualdade exagerada \( -1\ll w_i \ll 1\).
Assim, o treino levou as posições de \( W\) a assumirem valores com magnitudes contidas neste intervalo, tal que, por exemplo, se a imagem tiver predomínio de zeros, então, esperamos que
Este valor de \( y\), calculado para a combinação linear de pesos e posições da imagem com predomínio de zeros, concorda bastante bem com o intervalo que acabamos de ver que os \( w_i\) devem estar. Os poucos 1’s que aparecem no vetor \( x\) são multiplicados por pequenos \( w_i\), na maioria negativos, ou com a soma dos valores negativos excedendo em módulo aos valores positivos, e cuja soma acaba por ter o resultado ao qual chegamos em 24, o que também concorda com a metade inferior da forma íngreme de "s" da função sigmoid, estar sobre o lado negativo do eixo horizontal.
4. Múltiplas Camadas
Um Perceptron pode ter mais de uma camada e, geralmente, tem, principalmente, em modelos de Deep Learning.
É possível "empilhar" camadas! Isto é feito para melhorar a aprendizagem.
Quanto mais um perceptron associa corretamente os dados de treino, \( x\), com a sua correspondente resposta desejada, \( z\), melhor ele está aprendendo. O aumento estratégico do número de pesos da rede, através do aumento do número de camadas, pode melhorar o desempenho do treino, ou seja, \( E\) diminui, o que se traduz como melhora do aprendizado, isto é, mais pares \( (x,z)\in D\) são corretamente associados pelo perceptron.
4.1. A Propagação de um Sinal x Através das Camadas da Rede
Um sinal de entrada, \( x\), "fluirá" através das camadas da rede, entrando na primeira camada, passando por cada uma delas até sair através das funções de ativação da última camada.
Já vimos que um perceptron de uma única camada se define por seus pesos e bias, então, podemos encará-lo como sendo o objeto
Vamos representar o empilhamento de camadas, ou seja, a justaposição de vários perceptrons de uma camada só, simplesmente, assim:
em que
Os sobrescritos em 27 indicam o número da camada a qual pertencem os pesos e bias.
4.2. Um Perceptron de 2 Camadas
Vamos, por ora, considerar um perceptron de duas camadas, \( P=P_1\rightarrow P_2\). O perceptron 1 tem \( n\) neurônios, enquanto que o perceptron 2 terá \( p\) neurônios. Consideraremos um vetor de entrada, \( x\), com \( m\) elementos.
O perceptron \( P_1\) receberá o sinal \( x\), mas \( P_2\) receberá a saída de \( P_1\), isto é, as funções de ativação, \( a^1\), de \( P_1\).
A saída de \( P_2\) é entregue à função de erro. Ou seja, as funções de ativação, \( a^2\), de \( P_2\) são os argumentos da Função de Erro.
4.2.1. A Equação de um Perceptron de 2 Camadas
Escrevamos uma versão simplificada para a equação de \( P\). Utilizarei o mesmo símbolo \( P\), como em 11, para designar a saída da rede. Para maior clareza, utilizaremos o símbolo, \( \circ\), que é às vezes utilizado na representação da composição de funções.
As expressões de 28 exibem detalhes da estrutura compositiva de \( P\). Continuando,
As expressões em 29 são a continuação do desenvolvimento iniciado em 28 e elas mostram como o sinal de entrada, \( x\), é absorvido na linearidade, \( y^1\) e como, posteriormente, esta linearidade é absorvida pelo vetor de ativações de \( P_1\). Note, na primeira e última linhas, como \( y^1\) e \( a^1\) são vetores-coluna.
Já, as expressões em 30 mostram como as ativações, \( a^1\), da primeira camada entram na linearidade, \( y^2\), da camada 2.
4.2.2. A Função de Erro de Um Perceptron de 2 Camadas
Assim, escrevamos a função de erro de \( P\), explicitando a sua estrutura compositiva.
Novamente, os sobrescritos em 32 designam o número da camada a que pertencem \( W\), \( b\) ou \( a\), respectivamente. Esta equação nos dá a forma como a função do erro de \( P\) está composta.
Poderíamos expressá-la, de modo mais incompleto e menos informativo, mas mais compacto assim:
Embora, nenhuma das expressões em 33 explicite a localização e relações dos pesos e bias, elas deixam apreender, num só lance, a profundidade e a ordem da composição.
Preparando-se para Derivar a Função de Erro de Um Perceptron de 2 Camadas
A aprendizagem de um perceptron acontece através do ajuste dos seus pesos e este ajuste é feito ao final de um processo, que se repete muitas vezes, e que se inicia com o cálculo da derivada do estado atual da função de erro com relação a todos os pesos de uma rede, \(\frac{\partial E}{\partial W}\).
-
É importante, agora, frisarmos que:
-
O ajuste dos pesos acontece durante um processo chamado de retro-propagação ou propagação para trás. Quando um sinal \( x\) é apresentado à rede, \( P(x)\), ele "flui" para adiante ou para frente, através da rede, indo da primeira camada até a última. Por outro lado, quando o ajuste dos parâmetros treináveis é feito, o sinal de ajuste flui ou propaga-se para trás. Isto tem a ver com o fato de que quando derivamos, derivamos para trás. A derivação é aplicada às camadas mais externas da rede primeiro, ou seja, é aplicada às últimas camadas primeiro, e, daí, retrograde até a camada inicial. Isto ficará muito claro quando explicarmos o processo inteiro, em sua generalidade, a partir da Seção A Derivada do Erro com Relação aos Pesos de uma Camada Qualquer.
-
Queremos as derivadas de \( E\) com relação aos parâmetros treináveis, \( W=\{W^1, W^2\}\), de \( P=P_1\rightarrow P_2\) para que possamos retro-propagar o erro e realizar o aprendizado do perceptron.
-
Estes parâmetros encontram-se em profundidades diferentes dentro da rede. No nosso caso presente, \( W^2\) está na segunda ou última camada, enquanto que \( W^1\) são os pesos da primeira camada.
-
A derivação e a retro-propagação têm uma direção: elas vão da última camada para a primeira.
-
Assim, o cálculo da derivada de um perceptron de duas camadas é feito em duas partes. Primeiro calculamos \(\frac{\partial E}{\partial W^2}\) para só então calcularmos \(\frac{\partial E}{\partial W^1}\).
-
4.2.3. As Taxas de Variação do Erro
Acabamos de mencionar que há um conjunto de todos os pesos \( W=\{W^1 ,W^2\}\). O objetivo é derivar com relação a todos os pesos do Perceptron, mas, em etapas, de modo a ser possível calcular as atualizações dos pesos de \( W^2\) e depois as de \( W^1\) e, posteriormente, fazer o mesmo para os bias.
4.2.4. Derivada do Erro com Relação aos Pesos da Camada 2
Sem mais delongas, passemos à derivação de \( E(W^1,W^2,b^1,b^2)\) com relação aos pesos e bias da camada 2: \( W^2\) e \( b^2\). Os cálculos a seguir e comentários sobre os seus detalhes já foram feitos na Seção Gradiente do Erro com Relação a W. Portanto, aqui, a equação 15 é reescrita, adequando-se a sua notação a este caso de 2 camadas. Em ambos os casos, estamos lidando com a última camada da rede.
Note a diferença sutil entre 17 e a terceira linha de 34. Em 17, o vetor-coluna de matrizes mais à direita, continha as componentes de \( x\) ao longo da única linha não nula de cada matriz do vetor-coluna. Agora, a equação, na terceira linha de 34 contém, naquelas mesmas posições, os elementos do vetor de ativações, \( a^1\), da camada 1.
Note, também, que o processo de derivação \( \frac{\partial E}{\partial W^2}\) se estende apenas à camada 2, onde estão os pesos \( W^2\), entranhados na linearidade \( y^2\). Então, levando-se em conta a segunda linha de 28, podemos frisar que
Por fim, note que a última linha de 34, pode ser desenvolvida ainda mais, de modo a se obter uma forma final que não contenha aquele, desajeitado e difícil de manipular, vetor-coluna de matrizes.
Como vemos, abaixo, a forma final de \( \frac{\partial E}{\partial W^2}\) é bem reduzida e emprega a operação de produto externo, o que indicamos com o símbolo \( \otimes\).
O leitor, assim como este autor, provavelmente não acha natural ter, na última linha de 37, o vetor de derivadas de \( E\) sucedendo a matriz diagonal das derivadas de \( a^2\). Este é um pequeno preço a ser pago pela redução da forma e o aumento da facilidade de manipulação de 34. A comutação envolvida ali vem da transposição efetuada na segunda linha. Esta transposição se faz sentir na matriz diagonal e em \( \nabla_{a^2} E\), sendo que a matriz diagonal é idêntica à sua transposta.
Por um lado, as bibliotecas de manipulação de matrizes e vetores, como Numpy ou Tensorflow, proveem um método nativo para o produto externo. Por outro, a codificação de um vetor-coluna de matrizes, embora não seja difícil, pode consumir tempo em sua escrita e testes prévios de correção e bom funcionamento.
Mas, por fim, a efetivação do produto, que está dentro dos parênteses, na penúltima ou na última linhas de 37, nos leva a um vetor-coluna cujas entradas escalares são produtos de derivadas que podem ser ajeitadas de modo a exibir a ordem correta dos fatores, como se vê no vetor-coluna que está na primeira linha.
4.2.5. Derivada do Erro com Relação aos Bias da Camada 2
Agora, a derivada \( \frac{\partial E}{\partial b^2}\) tem a mesma forma que a primeira e segunda linhas de 19, com a exceção dos sobrescritos e também apenas atinge a primeira parte da rede.
4.2.6. Derivada do Erro com Relação aos Pesos da Camada 1
Agora, vamos calcular a derivada com relação a \( W^1\) e, logo em seguida, comentar sobre os seus elementos.
Já mencionamos que as linearidades \( y^1(x)\) e \( y^2(a^1)\) absorvem os seus respectivos sinais entrantes, \( x\) e \( a^1\), do mesmo modo. Isto pode ser visto claramente em 29 e 31. Elas são muito parecidas.
Mas, no cálculo de \( \frac{\partial E}{\partial W^1}\), elas acabam por ser derivadas com relação a elementos diferentes da estrutura de P. A linearidade \( y^2\) é derivada com relação às ativações da camada 1, enquanto que \( y^1\) é derivado com relação a todos os pesos, \( W^1\), de sua própria camada, 1. É assim que o objetivo de derivar \( E\) com relação a \( W_1\) é alcançado.
Por esta razão, \( \frac{\partial y^2}{\partial a^1}\) é uma matriz \( p\times n\), enquanto que \( \frac{\partial y^1}{\partial W_1}\) é um vetor-coluna com \( n\) elementos, cada um dos quais é uma matriz \( n\times m\).
Aliás, a matriz \( p\times n\), resultante do cálculo de \( \frac{\partial y^2}{\partial a^1}\), é precisamente a matriz de pesos \( W^2\). Isto pode ser visto em 41.
Mais uma vez, podemos simplificar a expressão final da derivada de \( E\). Consideremos o seguinte desenvolvimento a partir da penúltima linha de 41.
Tal desenvolvimento também levará a uma forma envolvendo um produto externo com o sinal entrante que, neste caso, é \( x\). Então, o cálculo pode continuar como feito abaixo, em 43.
Fazendo a soma indicada, obtemos
Note que na passagem da segunda para a terceira linhas de 44, reconhecemos que a expressão que foi transposta é a mesmíssima que aparece na terceira linha! Daí bastou "desempacotar" os fatores já conhecidos. No momento, a deixaremos como está. Mas, logo veremos que esta expressão pode ser ainda mais trabalhada e que ela fará parte da metodologia recursiva que utilizaremos para calcular as taxas de variação do Erro em Perceptrons de várias camadas.
Nós veremos que, em perceptrons de mais de 2 camadas, o padrão \( \frac{\partial a^{l+1}}{\partial y^{l+1}}\cdot W^{l+1}\cdot \frac{\partial a^l}{\partial y^l}\), em que \( l\) é o número de uma camada, se repete. Sempre haverá \( L\) repetições deste padrão, encaixadas entre o \( \nabla_{a^L} E\) inicial e a \( \frac{\partial y^1}{\partial W^1}\) final, para um perceptron de L camadas. Esta constatação nos ajudará a produzir uma fórmula geral para o cálculo das derivadas da função de erro, \( E\), para um perceptron de um número qualquer de camadas.
4.2.7. Derivada do Erro com Relação aos Bias da Camada 1
Por fim, a derivada de E com relação aos bias da 1ª camada. Novamente, o cálculo com relação aos viéses segue bem de perto o cálculo com relação aos pesos da mesma camada, sendo apenas mais simples, uma vez que \( \frac{\partial y^1}{\partial b^1}\) produz uma matriz unitária.
4.3. Um Perceptron de Múltiplas Camadas
Agora que já ganhamos uma melhor compreensão sobre a estrutura de um Perceptron, vamos, rapidamente, escrever a equação para um, \( P\), com um número qualquer de camadas, \( L\). Utilizamos novamente o símbolo, \( \circ\), de composição de funções.
As reticências, naturalmente, indicam que, em seu lugar podem estar um número qualquer de camadas e cada par \( a^l\circ y^l\) indica os elementos da camada \( l\), a saber, respectivamente, o vetor de ativações cujo argumento é o seu vetor de linearidades, \( a^l( y^l)\).
Com a exceção da linearidade da camada 1, cada outra linearidade, \( L\ge l\ge 2\), tem a seguinte forma
em que \( n_l\) e \( p_l\) são, respectivamente, o número de linhas e de colunas de \( W^l\). Como o número de colunas da matriz \( W^l\) e o número de linhas do vetor \( a^{l-1}\) coincidem, o número de elementos de \( a^{l-1}\) também é \( p_l\).
A linearidade da camada 1 tem a forma muito parecida com a das demais linearidades, com a exceção do seu sinal entrante, \( x\).
4.4. A Função de Erro de um Perceptron de Múltiplas Camadas
A função de erro para o caso de \( L\) camadas é a mesma que a dos demais casos. Ela toma como argumento a saída, \( P\), do Perceptron.
4.5. A Derivada do Erro com Relação aos Pesos de uma Camada Qualquer
Vamos, a seguir, exibir a fórmula da derivada de \( E\) com relação aos pesos de uma camada \( l\). A sua forma é perfeitamente apreensível quando se tem em vista a expressão 49, pois, a partir disto, sabemos que temos que utilizar a regra da cadeia como método de derivação para obtermos
enquanto que a derivada com relação aos pesos da camada 1, \( W^1\), é
Acontece que, por mais belas e elegantes que sejam 50 e 51, em muitos casos, elas não poderiam ser calculadas inteiras a cada passo do treino de um Perceptron de várias camadas!
Quanto mais camadas um perceptron tem, mais longas são 50 e 51. Lembremos que cada derivada nestas fórmulas é uma matriz ou vetor ou, ainda, um vetor de matrizes cujas dimensões podem tomar valores bem altos. Isto torna impraticável o uso destas fórmulas na forma em que estão.
Considere dois cálculos sucessivos, o de \( \frac{\partial E}{\partial W^{l+1}}\) e \( \frac{\partial E}{\partial W^{l}}\). Se fôssemos utilizar a fórmula 50 para estes dois cálculos, teríamos calculado todas as primeiras \( L-(l+1)+1=L-l\) taxas de variação de 50 duas vezes!
Felizmente, há uma solução prática para este problema.
4.6. Processo Prático Para a Atualização dos Pesos e Bias
A solução ao problema apresentado na seção anterior é calcular a derivada dos pesos de uma camada, \( l\), aproveitando todos os cálculos já feitos para as camadas \( L\) até \( l+1\). A cada passo na descida pelas camadas, guarda-se o último cálculo realizado na memória.
4.6.1. Derivada de E com Relação aos Pesos
Isto é feito da seguinte forma. Considere as expressões a seguir, todas equivalentes à derivada de E com relação aos pesos da camada L
De modo que, da segunda linha de 53, temos, necessariamente, 54 que é a parte que nos importa salvar, por ora, na memória para os próximos cálculos.
Agora, preste atenção no que farei com 54, pois vou multiplicá-la por
para obter
Analise com atenção o lado esquerdo da primeira equação de 56 e certifique-se de que ele realmente se reduz ao lado esquerdo da quarta equação, pois é vital entendermos que a multiplicação de matrizes que acabamos de fazer, realmente, produz a derivada de E com relação aos pesos da camada seguinte da rede, da última para a primeira, a saber, \( \frac{\partial E}{\partial W^{L-1}}\).
Do lado direito, na quarta linha de 56, temos a parte que devemos salvar na memória para realizarmos o próximo cálculo da derivada de \( E\), que será com relação a \( W^{L-2}\).
Antes de mais nada, utilizemos 54 para escrever
A segunda equação em 57 resulta de se realizar o produto matricial \( \frac{\partial E}{\partial a^L}\frac{\partial a^L}{\partial y^L}\) e mostra a natureza recursiva da derivada de \( E\) com relação às linearidades do Perceptron, pois ela mostra a dependência que \( \frac{\partial E}{\partial y^{L-1}}\) tem de \( \frac{\partial E}{\partial y^L}\). O método que estamos desenvolvendo é um método recursivo.
Este método prático funciona, pois o que estamos salvando na memória é apenas o resultado dos cálculos e não as matrizes cujo produto dá este resultado. E, ele continua deste modo até que calculemos a derivada do Erro com relação aos pesos da camada 1.
Então, raciocinando de forma indutiva, sempre que tivermos calculado a derivada do Erro com relação aos pesos de uma camada \( l+1\), já teremos obtido a derivada do Erro com relação à linearidade desta camada
Aí, neste ponto, calculamos a quantidade correspondente a 55, só que, agora, com relação à camada \( l\) e em dois passos. Primeiro, calculamos apenas a quantidade
cujo produto com 58 produz
Veja que, em 58, já realizamos o produto matricial \( \frac{\partial E}{\partial y^{l+2}}\frac{\partial y^{l+2}}{\partial a^{l+1}}\frac{\partial a^{l+1}}{\partial y^{l+1}}\) que esta indicado em 60.
Por fim, multiplicamos ambos os membros da segunda equação em 60 por \( \frac{\partial y^{l}}{\partial W^{l}}\) para obtermos
4.6.2. Derivada de E com Relação aos Bias
O processo de dedução da derivada da função de erro com relação aos bias de uma camada qualquer é basicamente o mesmo que seguimos até aqui para a derivação quanto aos pesos.
Seguindo-se os mesmos procedimentos, é possível constatar que, também no caso dos viéses, a derivada de \( E\) com relação à linearidade da camada \( l\), ou seja, \( \frac{\partial E}{\partial y^l}\), é a mesmíssima que encontramos em 60. Não deveria haver surpresa alguma quanto a este fato, já que os pesos e os bias da camada \( l\) estão entranhados na única e mesma linearidade desta camada da rede.
Por fim, para encontrarmos \( \frac{\partial E}{\partial b^l}\), multiplicamos, como antes, a equação 60, só que agora, por \( \frac{\partial y^l}{\partial b^l}\) para obtermos
Mas, já vimos em 19 que sempre teremos
de modo que a segunda equação em 62 é, simplesmente, idêntica a \( \frac{\partial E}{\partial y^l}\) como expresso abaixo
4.6.3. A Fórmula Geral
Ufa! Agora, estamos em condições de sumarizar o que deduzimos até aqui em uma fórmula geral para o cálculo da derivada do Erro com relação à linearidade de uma camada \( l\). Com ela se tornará muito simples calcularmos a derivada do Erro com relação aos pesos e bias de qualquer camada, seguindo o processo que descrevemos.
Veja que o caso \( l=L\) vem diretamente de 54, enquanto que o caso \( L>l\ge 1\) é a expressão à direita de 60.
De acordo com 64, a equação acima é a exata expressão que calcula \( \frac{\partial E}{\partial b^{l}}\) para qualquer camada de um Perceptron.
Para acharmos \( \frac{\partial E}{\partial W^l}\), as equações em 61 nos dizem que basta multiplicar 65, em ambos os lados, por \( \frac{\partial y^l}{\partial W^l}\) e ajeitar o lado esquerdo da expressão para chegarmos em
4.7. Analisando a Dimensão das Matrizes de \( \frac{\partial E}{\partial W^l}\) e de \( \frac{\partial E}{\partial b^l}\)
Vamos fazer uma rápida análise da dimensão das matrizes envolvidas em 66 e, em seguida, efetuar explicitamente os produtos indicados nela. Isto nos dará a imagem do resultado final dos cálculos que temos estado a realizar até este ponto. Além disto, este resultado será utilizado em 20 para a atualização dos pesos e, para isto, é preciso que as dimensões de \( W^l\) e de \( \frac{\partial E}{\partial W^l}\) sejam iguais.
Considerando os elementos estruturais e as camadas indicadas em 66, vamos supor que a camada \( l+1\) tenha \( n\) neurônios, que a camada \( l\) tenha \( p\) neurônios e que o número de elementos do vetor entrante, \( s\), seja \( m\). O vetor \( s\) é o sinal que entra na camada \( l\). Este sinal pode ser tanto o vetor de ativações da camada \( l-1\), como pode ser o vetor \( x\) sobre o qual a rede está sendo treinada. Se a camada \( l\) for a última camada da rede, então, \( s=x\), caso contrário, \( s=a^{l-1}\). Por esta razão, utilizarei o símbolo \( s\) no restante desta Seção para indicar que podemos estar tratando de qualquer um destes casos.
Neste caso, \( \frac{\partial E}{\partial a^l}\) é um vetor linha de \( p\) elementos, \( \frac{\partial a^{l}}{\partial y^{l}}\) é uma matriz quadrada \( p\times p\), enquanto que \( \frac{\partial y^l}{\partial W^l}\) é um vetor-coluna de \( p\) posições cujos elementos são matrizes com a mesma dimensão de \( W^l\), ou seja, \( p\times m\).
Agora, \( \frac{\partial E}{\partial y^{l+1}}\) é um vetor linha de \( n\) elementos, \( \frac{\partial y^{l+1}}{\partial a^{l}}\) é uma matriz \( n\times p\) e, por fim mas não menos importante, \( \frac{\partial E}{\partial W^l}\) é uma matriz com as dimensões de \( W^l\).
Havendo a necessidade, consulte a Seção Derivada de Funções Vetoriais no Apêndice para uma pequena explicação sobre a dimensão de objetos resultantes da derivação de funções vetoriais.
Então, no caso em que \( l=L\), temos um produto de três matrizes com as seguintes dimensões: \( 1\times p\), \( p\times p\) e \( p\times 1\). Isto é o mínimo que esperaríamos para que o produto fosse possível, que é, o número de colunas da matriz à esquerda ser igual ao número de linhas da matriz à direita.
No caso em que \( L>l\ge 1\), temos quatro matrizes com as seguintes dimensões, da esquerda para a direita: \( 1\times n\), \( n\times p\), \( p\times p\) e, por fim, \( p\times 1\). Novamente, temos o mínimo que precisaríamos ter.
Em ambos os casos, a dimensão final \( p\times 1\) é a de um vetor-coluna de \( p\) linhas e \( 1\) coluna, cujas \( p\) posições são matrizes que têm a dimensão de \( W^l\), como já vimos várias vezes até agora. Assim, em ambos os casos, a dimensão \( 1\times 1\) do resultado dos produtos matriciais não é um escalar, mas, antes, uma única matriz que, como vimos, tem a dimensão da matriz de pesos da camada \( l\), ou seja, \( p\times m\).
Então, quando \( l\) é a última camada da rede
É fácil de se perceber que a última linha em 68, e de fato todo o seu desenvolvimento desde 67, é, essencialmente, aquele que foi iniciado em 36, com a exceção dos símbolos do sinal entrante e do número da camada.
O produto externo não é tão comum quanto o produto normal de vetores, mas o seu conceito é tão simples quanto ele. Apresento a sua definição no Apêndice Produto Externo.
Agora, partamos para a explicitação de \( \frac{\partial E}{\partial W^l}\) para uma camada \( l\) qualquer, com exceção da última.
Na equação 39 e seguintes já havíamos visto que a derivada de uma linearidade com relação ao seu sinal de entrada é a matriz de pesos da camada desta linearidade. Então, em 69, já usamos o fato de que \( \frac{\partial y^{l+1}}{\partial a^l}=W^{l+1}\). Continuando,
Até aqui, fizemos o produto indicado de matrizes ou vetores, da esquerda para a direita. O leitor deve acompanhar estes desenvolvimentos bem de perto, já que eles são os responsáveis por produzir as formas matemáticas que tornam a aprendizagem possível em princípio. O vetor-coluna mais à direita é, em verdade o vetor vertical de matrizes, sobre o qual já temos estado a falar. Estas matrizes aparecerão explicitamente, logo abaixo.
A seguir, nós reencontraremos o vetor linha que encontramos na segunda expressão de 70, só que desta vez, ele estará encerrado dentro de uma operação de transposição. Esta expressão transposta é a responsável pela forma final à que chegaremos a abaixo.
Agora, vejamos as fórmulas correspondentes para os bias. Já vimos que a forma de \( \frac{\partial E}{\partial b^l}\) é mais simples que a de \( \frac{\partial E}{\partial W^l}\). Isto acontece pois \( \frac{\partial y^l_i}{\partial b^l}\) são matrizes unitárias e podem ser "desprezadas" no cálculo de \( \frac{\partial E}{\partial b^l}\). Assim, abaixo, apresento as fórmulas relativas aos viéses sem detalhar todo o seu desenvolvimento já que ele é análogo e mais simples do que o que acabamos de fazer.
Assim, a fórmula para os bias, se \( l\) é a última camada, é
Se \( l\) for qualquer outra camada exceto a última, então,
4.8. A Atualização dos Pesos e Bias
Já vimos em 20, 21, 22 e 23 como a atualização dos pesos e bias é feita. Vamos reproduzir aquelas fórmulas, aqui, carregadas com a informação que recém obtivemos sobre \( \frac{\partial E}{\partial W^l}\) e \( \frac{\partial E}{\partial b^l}\).
ou, ainda,
A primeira vez que vemos esta fórmula, podemos ter alguma surpresa em constatar a presença de pesos da camada \( l+1\) na atualização dos pesos da camada \( l\). E não são só os pesos. Os elementos do vetor \( \frac{d E}{d y^{l+1}}\) estão ali também. A natureza recursiva de \( \frac{d E}{d y^{l+1}}\), como mostrado na segunda equação de 60, nos faz compreender que, implicitamente, ela contém elementos de todas as camadas desde a última camada \( L\).
Isto é devido à retro-propagação do erro. A derivada de \( E\) começa a ser calculada com relação aos elementos da camada \( L\) e vai descendo, em cadeia, até a camada \( l\) desejada, e, no processo, evoca as precisas quantidades adequadas das outras partes da rede.
A fórmula para a atualização dos bias é, mais uma vez, mais simples do que a dos pesos.
ou seja,
Adicionei uma pequena continuação ao que foi exposto nesta seção aos Apêndices, na Seção Aprendizado Contínuo. Nela coloco algumas observações sobre o que pode ser chamado, provisoriamente, de aprendizado contínuo. O leitor interessado a terá à mão, mas ela não é indispensável ao entendimento do que apresentamos neste livro.
4.9. Dando Vida às Equações
4.9.1. Retropropagação a partir dos Princípios (Python/NumPy)
Este notebook implementa o nosso Perceptron de múltiplas camadas e o processo de aprendizagem usando apenas Python e a biblioteca NumPy para classificar imagens de algarismos manuscritos. O objetivo aqui é ver a teoria e as equações dos Capítulos 1, 2 e 3 o mais explicitamente possível.
Diferente do exemplo do próximo capítulo, aqui nós:
-
Não usaremos um framework de alto nível como o TensorFlow para o treino. Todo o cálculo será feito "na mão".
-
Treinaremos com um vetor de cada vez, em vez de lotes (veremos tudo sobre isto no Capítulo Treino em Lotes).
-
Implementaremos o cálculo do gradiente dos pesos, espelhando o mais perfeitamente possível a derivação matemática que vimos neste capítulo para um único exemplo de treino.
Este é o alicerce. Ao entender este código, você entenderá como os frameworks modernos usam, por baixo dos panos, a teoria que apresentamos.
4.9.2. Passo 1: Preparando o Ambiente e os Dados
Primeiro, preparamos nosso ambiente e dados. Usaremos NumPy para todos os nossos cálculos matemáticos e Matplotlib para visualização.
Por conveniência, usaremos a biblioteca tensorflow apenas uma vez para baixar o dataset MNIST (que contém o conjunto de imagens com os dígitos manuscritos) de forma simples. A partir do carregamento, todos os dados serão arrays NumPy e o TensorFlow não será mais utilizado.
O pré-processamento é idêntico ao do exemplo seguinte: normalizamos os pixels, "achatamos" as imagens em vetores e usamos one-hot encoding para as respostas desejadas.
1import numpy as np
2import matplotlib.pyplot as plt
3import tensorflow as tf # Usado APENAS para carregar o dataset convenientemente
4
5# Carregar o dataset MNIST
6(x_train, z_train), (x_test, z_test) = tf.keras.datasets.mnist.load_data()
7
8# Função para one-hot encoding usando apenas NumPy
9def to_one_hot(labels, num_classes=10):
10 return np.eye(num_classes)[labels]
11
12# Pré-processamento com NumPy
13x_train = (x_train.astype("float32") / 255.0).reshape(60000, 784)
14x_test = (x_test.astype("float32") / 255.0).reshape(10000, 784)
15
16z_train_one_hot = to_one_hot(z_train).astype('float32')
17z_test_one_hot = to_one_hot(z_test).astype('float32')
18
19print("Dados prontos e em formato NumPy!")1# Código de visualização com Matplotlib
2plt.figure(figsize=(10, 5))
3for i in range(10):
4 plt.subplot(2, 5, i + 1)
5 plt.imshow(x_train[i].reshape(28, 28), cmap='gray')
6 plt.title(f"Label: {z_train[i]}") # Usamos o z_train original para o título
7 plt.axis('off')
8plt.suptitle("Amostra dos Dados de Treino (MNIST)", fontsize=16)
9plt.show()
4.9.3. Passo 2: Definindo as Ferramentas (Funções)
Como não estamos usando uma classe de modelo como no Keras, precisamos definir todas as nossas "ferramentas" como funções separadas. Aqui, criaremos as funções de ativação (ReLU e Sigmoid) e suas respectivas derivadas, a função de custo (Erro Quadrado Médio) e sua derivada, e uma função para inicializar os pesos e biases da nossa rede.
1# Funções de Ativação e suas derivadas
2def relu(y):
3 return np.maximum(0, y)
4
5def relu_derivative(y):
6 return np.where(y > 0, 1, 0)
7
8def sigmoid(y):
9 return 1 / (1 + np.exp(-y))
10
11def sigmoid_derivative(a):
12 return a * (1 - a)
13
14# Função de Custo e sua derivada
15def mean_squared_error(z, P):
16 return np.mean((z - P)**2)
17
18def mean_squared_error_derivative(z, P):
19 return P - z
20
21# Função para inicializar os parâmetros da rede
22def inicializar_parametros(layer_dims):
23 W = {}
24 b = {}
25 for l in range(1, len(layer_dims)):
26 # Inicializamos com valores aleatórios pequenos para quebrar a simetria
27 W[l] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
28 b[l] = np.zeros((layer_dims[l], 1))
29 return W, b4.9.4. Passo 3: O Treino com Retropropagação Manual
Esta é a célula central do nosso exemplo. Aqui, implementamos o processo de aprendizagem tal como apresentamos neste capítulo. O loop externo itera através das "épocas" (passagens completas pelo dataset), e o loop interno itera sobre cada exemplo de treino individualmente.
Para cada imagem x e seu rótulo z:
-
Propagação para frente (Forward Pass): Calculamos a saída da rede
Ppassandoxpor todas as camadas, guardando os valores intermediáriosyea. -
Cálculo do Erro: Medimos o erro
Eda previsão. -
Backpropagation: Começando da última camada, calculamos os gradientes
∂E/∂We∂E/∂bpara cada camada, espelhando o máximo possível a teoria que apresentamos. -
Atualização: Subtraímos uma fração do gradiente (controlada pela taxa de aprendizagem) dos parâmetros atuais, ajustando a rede na direção que minimiza o erro.
1# --- Hiperparâmetros e Arquitetura ---
2taxa_aprendizagem = 0.01
3epocas = 5
4# A arquitetura: entrada 784 (número de elementos do vetor x) -> 1ª camada 128 nerônios -> 2ª camada 64 neurônios -> 3ª camada (de saída) 10 neurônios
5layer_dims = [784, 128, 64, 10]
6
7# --- Inicialização ---
8W, b = inicializar_parametros(layer_dims)
9num_camadas = len(layer_dims) - 1
10historico_custo = []
11
12print("Iniciando o treino em Python/NumPy...")
13for i in range(epocas):
14 custo_total_epoca = 0
15 # O loop interno itera sobre cada exemplo
16 for x, z in zip(x_train, z_train_one_hot):
17 # Remodelar x e z para serem vetores coluna
18 x = x.reshape(-1, 1)
19 z = z.reshape(-1, 1)
20
21 # --- 1. Forward Pass ---
22 ativacoes = {'a0': x}
23 linearidades = {}
24
25 a_anterior = x
26 for l in range(1, num_camadas + 1):
27 y = np.dot(W[l], a_anterior) + b[l]
28 linearidades[f'y{l}'] = y
29
30 if l == num_camadas: # Última camada
31 a = sigmoid(y)
32 else: # Camadas ocultas
33 a = relu(y)
34 ativacoes[f'a{l}'] = a
35 a_anterior = a
36
37 P = ativacoes[f'a{num_camadas}']
38 custo_total_epoca += mean_squared_error(z, P)
39
40 # --- 2. Backpropagation ---
41 # Gradientes para os pesos e biases
42 dE_dW = {}
43 dE_db = {}
44
45 # 'Semente' do Gradiente (para a última camada L)
46 dE_dP = mean_squared_error_derivative(z, P)
47 dP_dyL = sigmoid_derivative(P)
48 dE_dy = dE_dP * dP_dyL # Delta inicial
49
50 # Loop Reverso
51 for l in reversed(range(1, num_camadas + 1)):
52 a_anterior = ativacoes[f'a{l-1}']
53
54 # Gradientes da camada 'l'
55 # USANDO O PRODUTO EXTERNO, COMO NA TEORIA!
56 dE_dW[l] = np.outer(dE_dy, a_anterior)
57 dE_db[l] = dE_dy
58
59 # Propagar o erro para a camada anterior (se não for a primeira)
60 if l > 1:
61 y_anterior = linearidades[f'y{l-1}']
62 dE_da_anterior = np.dot(W[l].T, dE_dy)
63 da_anterior_dy_anterior = relu_derivative(y_anterior)
64 dE_dy = dE_da_anterior * da_anterior_dy_anterior
65
66 # --- 3. Atualização dos Parâmetros ---
67 for l in range(1, num_camadas + 1):
68 W[l] -= taxa_aprendizagem * dE_dW[l]
69 b[l] -= taxa_aprendizagem * dE_db[l]
70
71 # Fim da época
72 custo_medio = custo_total_epoca / len(x_train)
73 historico_custo.append(custo_medio)
74 print(f"Época {i + 1}/{epocas} - Custo Médio: {custo_medio:.6f}")
75
76print("Treino finalizado!")1plt.figure(figsize=(10, 6))
2plt.plot(historico_custo, marker='o')
3plt.xlabel("Época")
4plt.ylabel("Erro / Custo Médio")
5plt.title("Evolução do Erro Durante o Treino (Python/NumPy)")
6plt.grid(True)
7plt.xticks(range(epocas))
8plt.show()
1def forward_pass_teste(x, W, b):
2 a = x.reshape(-1, 1)
3 num_camadas = len(W)
4 for l in range(1, num_camadas + 1):
5 y = np.dot(W[l], a) + b[l]
6 if l == num_camadas:
7 a = sigmoid(y)
8 else:
9 a = relu(y)
10 return a
11
12def testar_modelo_numpy():
13 idx_aleatorio = np.random.randint(0, len(x_test))
14
15 img = x_test[idx_aleatorio]
16 label_real = z_test[idx_aleatorio] # Usamos o z_test original
17
18 vetor_predicao = forward_pass_teste(img, W, b)
19 label_predito = np.argmax(vetor_predicao)
20
21 plt.imshow(img.reshape(28, 28), cmap='gray')
22 plt.title(f"Predição do Modelo: {label_predito}\nRótulo Real: {label_real}")
23 plt.axis('off')
24 plt.show()
25
26# Execute esta célula várias vezes para testar!
27testar_modelo_numpy()5. Treino em Lotes
Neste capítulo descreveremos a matemática do treino em lotes que generaliza a descrição matemática da aprendizagem.
Ao invés de propagar um único sinal, x, a cada etapa de treino, podemos propagar vários vários deles reunidos em uma matriz que chamamos lote de vetores de treino. Daí, a expressão treinar em lotes.
Os modernos processadores computacionais permitem a realização simultânea, ou paralela, de muitos cálculos. Assim, no treino em lotes, pode-se calcular em paralelo a combinação linear de um sinal entrante com cada um dos vetores de pesos de uma mesma camada perceptrônica. Ou seja, é possível calcular a saída de todos os neurônios de uma mesma camada.
5.1. Treinando em Lotes
O treino em lotes consiste da utilização de lotes de vários vetores de treino, \( X\), ao invés de vetores únicos, \( x\), a cada etapa de propagação. O lote, \( X\) é, em verdade, uma matriz já que os \( x\) são vetores. Tenhamos em mente que um \( j-\text{ésimo}\) vetor \( x\) é a coluna, \( X^j\), da matriz \( X\).
5.1.1. O Efeito do Lote X na Primeira Camada
Vejamos qual é a expressão matemática disto. Reescrevamos a equação 9 com um lote (“batch” em inglês) de \( \beta\) vetores \( x\) para a primeira camada da rede. Este momento requer atenção para o fato de estarmos considerando a primeira camada da rede.
É claro que, agora, o vetor de linearidades da primeira camada é uma matriz e, para marcar esta diferença, usei outro símbolo, \( Y^1\).
Também, temos agora uma matriz de viézes e não mais apenas um vetor. Note que todas as colunas da matriz de viéses são iguais! Precisa ser! Pois, a rede neural ainda é a mesma, com a diferença de ser treinada sobre mais de um vetor de entrada ao mesmo tempo. Cada vetor de entrada no lote combina-se ainda com os mesmos pesos e o mesmo bias definidores da rede!
Usa-se, agora, uma matriz de viéses com \( \beta\) vetores-coluna idênticos, ou seja, \( B^1=\cdots=B^k=\cdots=B^{\beta}\). Isto é assim, para se manter a coerência com o jeito que matrizes e vetores se operam matematicamente, mas a igualdade entre os vetores coluna da matriz B já nos mostra que ainda temos um único vetor de bias aprendendo e que este vetor único é aplicado a cada um dos \( \beta\) conjunto de cálculos ocorrendo em paralelo para se tratar os \( \beta\) vetores distintos do lote de treino.
onde, agora, os elementos \( Y^j\) são as \( \beta\) colunas de \( Y^1\); \( W_i\) são as linhas de \( W\) e \( X^j\) é a \( j-\text{ésima}\) coluna do lote \( X\). O sobrescrito \( 1\), nos membros à esquerda de 80, indica o número da camada. Assim, qualquer um dos elementos da matriz \( Y^1\) pode ser representado por
As expressões à esquerda em 80 nos mostram que a linearidade da camada 1 deixou de ser um vetor-coluna para ser uma matriz de \( \beta\) vetores-coluna.
Então, agora, devemos aplicar as funções de ativação à saída de 80, ou seja, calcularemos as funções de ativação sobre cada um dos \( \beta\) vetores coluna \( Y^j\). Com a exceção de tratar-se de um lote de vetores, o cálculo das ativações está como antes, isto é, a ativação é aplicada à cada vetor de linearidades, \( Y^j\), de uma camada da rede que, por sua vez, é a resposta a um vetor de treino \( X^j\).
onde \( A\) é o novo símbolo para as ativações, que não são mais um único vetor-coluna, mas uma matriz de vetores-coluna. O mesmo vale para \( P\) como mostram as três equações acima.
Resumindo, treinar a rede em lotes, significa calcular simultaneamente a resposta da rede para cada um dos vetores do lote de entrada. Se a entrada, \( X\), é constituída de \( \beta\) vetores, então, naturalmente, a saída da rede é uma matriz, também, de \( \beta\) vetores \( Y^j\) - uma resposta para cada entrada \( X^j\).
5.1.2. O Efeito do Lote X Numa Camada Qualquer
Acontece que, como já destacamos na segunda e terceira expressões em 82, a saída da camada 1 é uma matriz. Isto significa que a entrada da camada 2 é esta mesma matriz. É claro que isto acontecerá a todas as demais camadas da rede e, em verdade, podemos mostrar isto apenas trocando o lote de entradas, \( X\), por uma matriz de sinais entrantes, \( S\), em 80 para obtermos
em que a notação sobrescrita aos colchetes, \( l\), indica o número da camada do elemento de rede.
A fórmula 83 é a mesma que vemos na última expressão de 80 e elas mostram que se uma camada, \( l\), receber uma matriz de \( \beta\) vetores-coluna como argumento, então, esta camada \( l\) dará outra matriz de \( \beta\) vetores-coluna como resposta que, por sua vez, será o sinal de entrada da camada \( l+1\), e assim por diante.
Além disto, das duas expressões em 83, vê-se que a contabilidade dimensional do produto matricial é respeitada em cada camada da rede, sendo este um dos aspectos que possibilita o uso de lotes. A matriz de pesos é \( n\times m\) enquanto que \( S^{l-1}\) é \( m\times \beta\), onde \( m\) é o número de elementos no vetor entrante, o qual coincide com o número de colunas de \( W^l\). Cada vetor-coluna \( B^k\) tem, naturalmente, n elementos.
Deste modo, mostramos como é que um sinal matricial de entrada, \( S\), flui através de um Perceptron, mantendo constante o número de colunas até sair pela última camada da rede, ponto em que será entregue à Função de Erro.
Não é demais destacar que uma matriz de sinais entrantes, \( S\), pode ser tanto uma matriz de vetores de treino, \( X\), como uma matriz de vetores-coluna de ativações, \( A\), advinda da camada anterior. Se a camada em questão for a camada 1, então, \( S=X\), caso contrário, \( S=A^{l-1}\).
5.1.3. A Equação do Perceptron Teinado em Lotes
Então, se fôssemos escrever uma equação geral para um Perceptron de Múltiplas Camadas, inspirada na fórmula 46, mas com a notação matricial que utilizamos neste capítulo, teríamos
onde, como em 46, os sobrescritos indicam o número das camadas.
5.1.4. O Erro como Uma Média Aritmética
Como já mencionamos, no caso de treino em lotes, a função de erro agirá sobre uma matriz de várias colunas e não mais apenas sobre um vetor-coluna. Como veremos, em seguida, a Função de Erro aplicada sobre uma matriz (cujas colunas são os vetores de ativação da última camada), acaba por ser calculada como a média aritmética dos erros cometidos por cada vetor-coluna na matriz de ativações. Lembremos que cada vetor de ativações é a resposta da rede a um dos vetores-coluna do lote.
Embora, a Função de Erro neste caso de treino em lotes seja diferente da Função de Erro que vínhamos vendo até agora, no aspecto geral, como antes, ela é
onde \( W=\{W^L, W^{L-1},\dots, W^1\}\).
Embora diferente, a função de Erro, \( E\), no caso de treino em lotes ainda é uma medida de quão próximos os vetores-coluna da saída, \( P\), da rede estão das respostas corretas e correspondentes a cada vetor-coluna do lote de treino, \( X\). Mostramos, no Apêndice A Função de Custo sobre um Domínio Matricial é uma Norma, que esta nova Função de Erro é, de fato, também uma norma, se \( E_j\) (ver abaixo) for uma norma. Agora, como antes, \( E\) é uma função de valor real, mas, diferente de antes, com domínio matricial. Podemos simbolizar isto assim: \( E:\mathbb{R}^{r\times \beta}\longrightarrow \mathbb{R}\), em que \( \mathbb{R}^{r\times \beta}\) simboliza o conjunto de matrizes com \( r\) linhas e \( \beta\) colunas, cujas entradas são números reais.
Deste modo, podemos mostrar 85 sob uma forma ainda mais reduzida, sem ressaltar a sua natureza compositiva, mas realçando o fato de que a função de ativações da última camada da rede, \( A^L\), é uma matriz, que \( E\) depende dos pesos atuais de \( W\) e, principalmente, que \( E\), agora, toma a forma de uma média aritmética dos erros calculados sobre cada uma das colunas de \( A^L\).
Aqui, os sobrescritos designam o número de uma coluna da matriz \( A\) da última camada da rede. \( E_j\) é o erro como o vínhamos vendo até o capítulo anterior, ou seja, uma função real sobre um vetor-coluna de ativações. Deste modo, vemos que a nova Função de Erro, necessária no treino em lotes, está intimamente relacionada à Função de Erro que havíamos considerado até agora, ou seja, a equação 49.
5.1.5. Treino em Lotes e a Taxa de Variação do Erro
Como se vê em 86, a aferição do desempenho do Perceptron, ainda vem de se conhecer o valor de cada erro, \( E_j\), associado a cada vetor de entrada, \( X^j\), do lote.
Tal aferição nos leva ao cálculo da derivada do erro e ao posterior processo de retro-propagação que torna possível ao Perceptron aprender. Então, passemos à derivada de 86 com relação aos parâmetros treináveis, \( W^l\), da camada \( l\).
Na segunda e terceira equações de 87, empregamos a utilíssima fórmula geral, 66, para o cálculo da derivada do erro com relação aos parâmetros treináveis de qualquer camada, \( \frac{\partial E_j(A^j)}{\partial W^l}\) (expressão a qual chegamos em 87), quando a rede é treinada sobre um único vetor se entrada, \( x\), pois vimos que o erro em domínio matricial se baseia no erro, \( E_j\), de domínio vetorial, o qual já havíamos calculado em 66.
Por fim, com base em 65 e com raciocínios análogos aos feitos logo acima, chegamos à forma abaixo para a taxa de variação do erro com relação aos bias de qualquer camada no treino em lotes.
5.2. A Atualização dos Parâmetros Treináveis no Treino em Lotes
Aqui, mais uma vez, a forma contida em 20 é a receita para a atualização dos pesos e a taxa de variação do erro com relação a eles tem a forma contida em 87, ou seja,
o que, de acordo com 76, nos leva a
É muito fácil de se ver que a equação 90 utiliza a forma de 76. A única diferença é que, agora, marcamos \( E\) e \( s\) com o número do vetor-coluna, \( j\), a que estes elementos correspondem no lote de treino.
As terceira expressão, em 89, nos deixa constatar que as \( \beta\) instâncias da rede, calculadas em paralelo, cada uma sobre um dos elementos do lote, \( X\), utilizam os mesmos elementos da rede. Vemos que elementos "concretos" como os pesos ou elementos dinâmicos como a forma da variação das ativações, por exemplo, são as mesmas para as \( \beta\) parcelas, embora o valor numérico, no caso das variações dinâmicas, possa mudar de acordo com o elemento do lote.
Mais uma vez, a forma da atualização respectiva ao bias é obtida por meio de procedimentos muito análogos aos feitos acima, mas a partir das equações 65, 78 e 88.
e
5.3. Dando Vida às Equações
5.3.2. Arquitetura e Componentes do Modelo
Antes de escrever o código, vamos detalhar a arquitetura do Perceptron que construiremos para resolver o problema do MNIST. O modelo que vamos implementar é um reflexo direto da teoria de múltiplas camadas e do processo de aprendizagem que exploramos.
O modelo é um Perceptron de múltiplas camadas, seguindo a estrutura geral de composição de funções aninhadas, como descrito na equação 46. O vetor de entrada, x, com os 784 pixels de cada imagem, flui pelas três camadas da rede. Cada camada implementa a operação de linearidade fundamental y = Wx + b, como vimos em sua forma mais básica em 6, seguida por uma função de ativação não-linear para adicionar poder de representação ao modelo.
Especificamente, nossa arquitetura é a seguinte:
-
Primeiras Camadas: A primeira camada oculta possui 128 neurônios, e a segunda possui 64. Para estas camadas, utilizamos a função de ativação ReLU (Rectified Linear Unit), uma escolha moderna e eficiente para evitar o problema do desaparecimento dos gradientes.
-
Camada de Saída: A camada final é composta por 10 neurônios, um para cada classe de dígito (0 a 9). Nesta camada, aplicaremos a função Sigmoid, que mapeia a saída de cada neurônio para um valor entre 0 e 1. Ambas as funções, ReLU e Sigmoid, estão detalhadas na tabela de Funções de Ativação A fórmula de algumas funções de ativação.
-
Função de Custo: Para medir o erro
Eentre a predição da redePe a resposta desejadaz, utilizaremos a função de custo Erro Quadrado Médio (MSE). Como estamos treinando em lotes, o erro final que otimizamos a cada passo é a média dos erros individuais de cada exemplo no lote, um conceito formalizado em 86. A fórmula base para o MSE pode ser encontrada na tabela de Funções de Custo A derivada de algumas Funções de Custo.
Com esta estrutura definida, o código que se segue irá traduzir cada um destes componentes em uma classe funcional do TensorFlow.
Este notebook é, de algum modo, a continuação do nosso exemplo anterior. Agora, veremos como os frameworks de alto nível facilitam e asceleram o treino com sua tecnologia de processamento paralelo.
Para aproveitarmos esta tecnologia que permite o treino em lotes otimizado e ainda exemplificarmos o uso das equações que aprendemos, vamos "abrir a caixa-preta" da função tape.gradient() e implementar nós mesmos o algoritmo de retropropagação (backpropagation) que foi deduzido matematicamente no livro.
O objetivo é demonstrar que as equações para ∂E/∂W e ∂E/∂b não são apenas teoria. Elas são o algoritmo.
Para isso, vamos:
-
Modificar nosso modelo para que ele nos dê as ativações e linearidades de cada camada.
-
Criar um loop de treino que calcula manualmente os gradientes para cada camada, de trás para frente, usando as fórmulas 87 e 88.
-
Usar o otimizador do TensorFlow apenas para aplicar os gradientes que nós mesmos calculamos.
Esta é a conexão profunda e explícita entre a matemática do aprendizado e sua implementação computacional.
1# Passo 1: Importar as bibliotecas necessárias
2import tensorflow as tf
3import numpy as np
4import matplotlib.pyplot as plt
5
6# Passo 2: Carregar o dataset MNIST
7(x_train, z_train), (x_test, z_test) = tf.keras.datasets.mnist.load_data()
8
9# Passo 3: Pré-processamento dos Dados
10# 3.1 - Normalização e Achatamento (Flattening)
11x_train = (x_train.astype("float32") / 255.0).reshape(60000, 784)
12x_test = (x_test.astype("float32") / 255.0).reshape(10000, 784)
13
14# 3.2 - One-Hot Encoding das Respostas Desejadas (z)
15z_train = tf.keras.utils.to_categorical(z_train, num_classes=10)
16z_test = tf.keras.utils.to_categorical(z_test, num_classes=10)
17
18# DEPOIS, garantimos que o tipo do array seja float32 usando .astype()
19z_train = z_train.astype('float32')
20z_test = z_test.astype('float32')
21
22print("Dados prontos para o treino!")1# Vamos visualizar algumas imagens para entender com o que estamos trabalhando.
2plt.figure(figsize=(10, 5))
3for i in range(10):
4 plt.subplot(2, 5, i + 1)
5 plt.imshow(x_train[i].reshape(28, 28), cmap='gray')
6 plt.title(f"Label: {np.argmax(z_train[i])}")
7 plt.axis('off')
8plt.suptitle("Amostra dos Dados de Treino (MNIST)", fontsize=16)
9plt.show()
1# A classe do Perceptron foi modificada para retornar os valores intermediários
2# (linearidades 'y' e ativações 'a'), que são cruciais para a retropropagação.
3
4class Perceptron(tf.keras.Model):
5 def __init__(self, layer_sizes):
6 super(Perceptron, self).__init__()
7 self.num_camadas = len(layer_sizes)
8 self.camadas = []
9 for units in layer_sizes:
10 self.camadas.append(tf.keras.layers.Dense(units, activation=None))
11
12 def call(self, x, return_internals=False):
13 """
14 Forward pass modificado. Se return_internals=True, ele retorna
15 a saída final e listas com as linearidades (y) e ativações (a) de cada camada.
16 """
17 a = x
18
19 # COMENTÁRIO ADICIONADO:
20 # Iniciamos a lista de ativações com a própria entrada `x`.
21 # Consideramos `x` como a 'ativação da camada 0' (a^0).
22 # Isso simplifica o acesso à 'ativação anterior' (a^{l-1}) no loop de retropropagação.
23 ativacoes = [a]
24 linearidades = []
25
26 # Camadas ocultas com ReLU
27 for camada in self.camadas[:-1]:
28 y = camada(a)
29 a = tf.nn.relu(y)
30 linearidades.append(y)
31 ativacoes.append(a)
32
33 # Última camada (saída)
34 y_final = self.camadas[-1](a)
35 P = tf.nn.sigmoid(y_final)
36 linearidades.append(y_final)
37 ativacoes.append(P)
38
39 if return_internals:
40 return P, linearidades, ativacoes
41
42 return P 1# --- Hiperparâmetros e Instâncias ---
2taxa_aprendizagem = 0.001
3epocas = 10
4tamanho_lote = 64
5
6modelo = Perceptron(layer_sizes=[128, 64, 10])
7# otimizador = tf.keras.optimizers.Adam(learning_rate=taxa_aprendizagem)
8# Descida Estocástica do Gradiente (em inglês: Stochastic Gradient Descent)
9otimizador = tf.keras.optimizers.SGD(learning_rate=taxa_aprendizagem)
10funcao_custo = tf.keras.losses.MeanSquaredError()
11
12# --- Preparando os lotes de dados ---
13dataset_treino = tf.data.Dataset.from_tensor_slices((x_train, z_train))
14dataset_treino = dataset_treino.shuffle(buffer_size=60000).batch(tamanho_lote)
15
16# --- Loop de Treino ---
17historico_custo = []
18
19print("Iniciando o treino com retropropagação 100% explícita com nossas fórmulas...")
20for epoca in range(epocas):
21 custo_medio_epoca = tf.keras.metrics.Mean()
22
23 for x_lote, z_lote in dataset_treino:
24
25 P_lote, linearidades, ativacoes = modelo(x_lote, return_internals=True)
26 E = funcao_custo(z_lote, P_lote)
27
28 # ==========================================================
29 # 3. BACKPROPAGATION CODIFICADA MANUALMENTE PARA EXPLICITAR
30 # E ESPELHAR AS EQUAÇÕES QUE DEDUZIMOS.
31 # ==========================================================
32
33 dE_daL = P_lote - z_lote
34 aL = ativacoes[-1]
35 daL_dyL = aL * (1 - aL)
36 dE_dy = dE_daL * daL_dyL
37
38 gradientes_finais = []
39
40 for l in reversed(range(modelo.num_camadas)):
41 camada = modelo.camadas[l]
42
43 # COMENTÁRIO ADICIONADO:
44 # A ativação da camada anterior (a^{l-1}) é necessária para o cálculo do gradiente.
45 # Devido à forma como construímos a lista `ativacoes`, onde ativacoes[0] = a^0 (a entrada 'x'),
46 # para a camada 'l' do modelo (que é 0-indexed), a ativação anterior a ela
47 # está convenientemente armazenada em ativacoes[l].
48 a_anterior = ativacoes[l]
49
50 # COMENTÁRIO ADICIONADO:
51 # Este é o passo mais crucial, onde a teoria se conecta com a implementação eficiente.
52 # A equação do livro para dE/dW^l (para um exemplo) é um produto externo.
53 # Para um LOTE, precisamos da SOMA dos produtos externos de cada exemplo.
54 # A multiplicação de matrizes (a_anterior^T @ dE_dy) é a forma
55 # matematicamente equivalente e computacionalmente otimizada de se fazer isso.
56 # Análise das Formas: [entradas, lote] @ [lote, saídas] -> [entradas, saídas], que é a forma de W^l.
57 dE_dW = tf.matmul(a_anterior, dE_dy, transpose_a=True)
58
59 dE_db = tf.reduce_sum(dE_dy, axis=0)
60
61 gradientes_finais.insert(0, dE_db)
62 gradientes_finais.insert(0, dE_dW)
63
64 if l > 0:
65 dE_da_anterior = tf.matmul(dE_dy, camada.kernel, transpose_b=True)
66 derivada_relu = tf.cast(linearidades[l-1] > 0, dtype=tf.float32)
67 dE_dy = dE_da_anterior * derivada_relu
68
69 otimizador.apply_gradients(zip(gradientes_finais, modelo.trainable_variables))
70 custo_medio_epoca.update_state(E)
71
72 historico_custo.append(custo_medio_epoca.result())
73 print(f"Época {epoca + 1}/{epocas} - Custo Médio: {custo_medio_epoca.result():.4f}")
74
75print("Treino finalizado!")1# Plotar o gráfico da função de custo
2plt.figure(figsize=(10, 6))
3plt.plot(historico_custo, marker='o')
4plt.xlabel("Época")
5plt.ylabel("Erro / Custo Médio")
6plt.title("Evolução do Erro Durante o Treino (Backprop Manual)")
7plt.grid(True)
8plt.xticks(range(epocas))
9plt.show()
1def testar_modelo():
2 idx_aleatorio = np.random.randint(0, len(x_test))
3 img = x_test[idx_aleatorio]
4 label_real = np.argmax(z_test[idx_aleatorio])
5
6 img_para_previsao = np.expand_dims(img, axis=0)
7
8 vetor_predicao = modelo(img_para_previsao)
9 label_predito = np.argmax(vetor_predicao)
10
11 plt.imshow(img.reshape(28, 28), cmap='gray')
12 plt.title(f"Predição do Modelo: {label_predito}\nRótulo Real: {label_real}")
13 plt.axis('off')
14 plt.show()
15
16# Execute esta célula várias vezes para testar!
17testar_modelo()Apêndice A: Norma Sobre Um Espaço Vetorial
Definição 1:
Norma é qualquer função real \( N(x)\) definida sobre um espaço vetorial \( V\) e que obedeça às três condições abaixo:
-
\( N(x)> 0,\ se\ x\ne 0\)
-
\( N(a\cdot x)=N(a)\cdot N(x)=|a|\cdot N(x)\)
-
\( N(x+y)\le N(x)+N(y)\) (Desigualdade Triangular)
com \( x,y\in V\) e \( a\in \mathbb{R}\).
Não definirei, aqui, o que seja um espaço vetorial por fugir muito do escopo deste livro. Basta que tenhamos utilizado vetores e matrizes pesadamente neste livro por seu significado direto e utilidade imediata. A sua definição pode ser encontrada online e em um sem número de livros de Álgebra Linear.
Prova:
Pelo item 1, \( N(x)\) é sempre positiva, exceto quando \( x=0\). Se \( x=0\), então, podemos escrevê-lo assim: \( 0\cdot x=0\). Neste caso, o item 2 da definição 1, nos dá \( N(0\cdot x)=N(0)\cdot N(x)=0\cdot N(x)=0\). Logo, \( N(x)\) só pode assumir valores positivos ou ser nula. Então o mínimo valor de \( N\) é \( 0\) e ele, como vimos, ocorre no vetor \( 0\).
Corolário:
A diferença \( x-y\) deve ser nula se a norma \( N(x-y)\) atinge o seu valor mínimo.
Prova:
A validade deste corolário é evidentíssima à luz da Proposição 1. Mas, suponhamos, por contradição, que \( x-y\) fosse diferente de zero quando \( N\) atingisse o seu mínimo. Então, teríamos \( N(x-y)=0\) com \( x-y\ne 0\). Mas, isto contrariaria o requisito 1 da Definição 1. Logo, \( N\) não seria uma norma.
Apêndice B: As Derivadas de \( y_i\)
B.1. A Derivada de \( y_i\) com Relação aos pesos \( W_i\)
Comecemos recordando que \( W_i=[w_{i1},\dots ,w_{ip}]\) é o vetor que está na linha \( i\) de \( W\).
Deste modo, também fica claro porquê \( \frac{\partial y_i}{\partial W_l}=0\) com \( i\ne l\). Pois, \( y_i\) simplesmente não depende de \( W_l\) e, assim, \( \frac{\partial (w_{ij}s_j +b_i)}{\partial w_{lj}}\) precisa ser nulo para todo o \( j\).
B.2. A Derivada de \( y_i\) com Relação aos bias \( b\)
Considere o vetor de bias \( b=[b_{1},\dots ,b_{n}]\). Desde que \( b\) é um vetor, podemos, naturalmente, calcular \( \nabla_b y_I\) para um \( i=I\) fixo. Só que este cálculo não é o mais adequado a ser realizado.
O Perceptron tem uma estrutura e, de acordo com esta estrutura, ele tem um único viés por neurônio. Isto quer dizer que a cada vetor \( W_I\), numa linha de \( W\), corresponde apenas um escalar \( b_I\). Isto produz o interessante resultado de os elementos não nulos de \( \nabla_b y_i\), com \( 1\le i\le n\), não estarem, de fato, ao longo de uma linha ou de uma coluna de \( \frac{\partial y}{\partial b}\), mas sim ao longo de sua diagonal principal (como mostrado na segunda e terceira expressões em 19)! Assim,
onde \( \frac{\partial y_I}{\partial b_i}=0\) com \( i\ne I\), enquanto que \( \frac{\partial y_I}{\partial b_i}=1\) se \( i=I\). Deste modo, escrevemos \( 1_I\) para indicar que a unidade só ocorre na posição \( I\) e que todas as demais posições são nulas.
Apêndice C: Derivada de Funções Vetoriais
Este pequeno resumo não trata da teoria das derivadas de funções vetoriais. Eu apenas apresento algo de notações e fatos relevantes para o assunto deste livro na esperança de que a memória do leitor complete o resto.
Para começar, considere uma função \( f:\mathbb{R}\rightarrow\mathbb{R}\), tal que \( y=f(x)\), de modo que \( f\) tem apenas um argumento.
Podemos representar a derivada de \( f\) como \( \frac{dy}{dx}\) ou \( \frac{df(x)}{dx}\), ou ainda de outras maneiras.
Agora, se a função for tal que \( y=f(x_1,\dots,x_n)\), ou seja, \( f: \mathbb{R}^n\rightarrow \mathbb{R}\), então, \( f\) tem \( n\) argumentos e, neste texto, representamos a sua derivada muito simplesmente assim \( \frac{\partial f}{\partial x}\), ou assim \( \nabla f\). Estes dois últimos símbolos representam um vetor e \( x=[x_1, \dots ,x_n\)].
A derivação transforma, de fato, uma \( f: \mathbb{R}^n\rightarrow \mathbb{R}\) em um vetor de modo que
Note o fato importante de que a \( f\) é uma função que leva pontos de um espaço de \( n\) dimensões para um espaço de uma dimensão e que - observe bem este fato - a derivada \( \frac{\partial f}{\partial x}\) é um vetor de uma linha e \( n\) colunas. Guarde bem esta observação.
Agora, considere uma função que leve um espaço de \( n\) dimensões num espaço de \( m\) dimensões, \( f: \mathbb{R}^n\rightarrow \mathbb{R}^m\), tal que
A derivação desta função resulta na seguinte matriz
Note que esta matriz tem \( m\) linhas e \( n\) colunas, pois o domínio da função é um espaço de \( n\) dimensões e o contra-domínio é um espaço de outras \( m\) dimensões.
Assim, o número de dimensões do domínio, determina o número de colunas, enquanto que o número de dimensões do contra-domínio determina o número de linhas da matriz resultante da derivação.
Veja que este fato vale para funções comuns, cujo domínio e contra-domínio são espaços de única dimensão, como no primeiro exemplo. A derivada \( \frac{df(x)}{dx}\) é uma matriz de uma linha e uma coluna, ou seja, um número escalar.
Neste texto, acabamos lidando com alguns objetos mais interessantes, tal como a derivada de uma função vetorial com relação a uma matriz inteira.
A função de uma rede neural pode ser um objeto grandioso e intrincado. Assim, temos que utilizar o poderio matemático a fim de descrever e operar com e sobre ele, de modo que a sua manipulação fique facilitada e o seu sentido esclarecido.
Neste caso, claramente, a matriz \( W\) é o argumento da função vetorial:
A derivada desta função segue a mesma “regrinha” que já usamos até aqui.
Consideramos, num primeiro momento, a matriz \( W\), de \( q\) linhas e \( r\) colunas, como um bloco único. Assim, a derivada da função acima, gerará uma matriz de \( m\) linhas e 1 coluna. Deste modo,
Note que os elementos do vetor-coluna acima são, de fato, matrizes.
Note bem que uma matriz é um vetor-coluna cujos elementos são as linhas desta matriz.
Por esta razão, podemos escrever qualquer um dos elementos do vetor-coluna 99 como
onde \( W_i\) representa o vetor que está na linha \( i\) da matriz \( W\).
Deste modo, 99 assume a seguinte bela e interessante forma:
Apêndice D: Algumas Observações sobre o Gradiente
Resultados muito interessantes surgem no entrecruzamento de conceitos de Álgebra Linear e de Cálculo.
Primeiro, do trato com vetores, sabemos que o produto interno entre dois vetores, \( c\) e \( d\) é
e que, portanto, o lado direito é máximo quando \( \cos\theta=1\), uma vez que \( -1\le \cos\theta\le 1\).
Mas, \( \cos\theta=1\), quando \( \theta=0\), ou seja, \( c\cdot d\) é máximo quando c e d são paralelos ou colineares ou, ainda, de mesma direção.
Por outro lado, a derivada direcional, \( \nabla_d f\), de uma função real \( f:\mathbb{R}^n\rightarrow\mathbb{R}\) na direção de um vetor unitário, \( d\), pode ser apresentada como o produto interno entre o gradiente de \( f\) e o vetor \( d\), assim
onde, usamos o fato assumido de que \( |d|=1\).
Agora, da discussão em torno de 102, sabemos que a segunda expressão em 103 será máxima quando \( \theta=0\) e, neste caso, teremos que quando a derivada direcional de uma função é máxima, esta derivada direcional coincide com o módulo do gradiente desta mesma função. Além disto, como \( \theta=0\), \( \nabla_d f\) e \( d\) têm ambos a mesma direção. Disto decorre que \( \nabla_d f\) tem a mesma direção de \( \nabla f\), uma vez que podemos escrever o vetor unitário \( d\) assim \( d=\frac{\nabla f}{|\nabla f|}\).
Vimos várias vezes neste livro que o vetor gradiente é composto das derivadas parciais de uma função. A soma destas derivadas parciais dá, de algum modo, a magnitude da taxa de variação total da função.
Pensando geometricamente, no familiar espaço tridimensional, quanto mais íngrime é a direção da reta tangente à uma função, maior é a sua taxa de variação. Assim, se, como acabamos de ver, \( \nabla f\) aponta na direção da maior taxa de variação de \( f\), então, \( -\nabla f\) apontará na direção da menor taxa, contanto que o ponto em que ela estiver sendo calculada não seja um ponto de sela ou um ponto de cunha.
Apêndice E: Produto Externo
Por fim, há também o produto externo cuja operação tem o seguinte símbolo: \( \otimes\). Tomemos, agora, os vetores \( c\) e \( e\) e os consideremos, respectivamente, como uma matriz de \( 1\) linha e \( m\) colunas; e outra matriz de \( n\) linhas e \( 1\) coluna. Note que, para o produto externo, os números de elementos em cada vetor não precisam ser iguais.
Então, a definição do produto externo é simplesmente
Assim, o resultado de um produto externo é uma matriz. Isto é assim pois os números escalares de \( e\) são as linhas da matriz \( e\), enquanto que os escalares de \( c\) são as colunas da matriz \( c\).
Apêndice F: Aprendizado Contínuo
O que vamos expor, aqui, é muito mais a colocação de um problema e a representação, em linhas muito gerais, de um princípio de solução. Há uma conjectura que está implicitamente sugerida nas fórmulas, 76 e 78, dos pesos e bias. Esta conjectura é a seguinte: elas podem ser mostradas, como veremos a seguir, sob a forma explícita de uma somatória cujas parcelas têm todas um pequeno coeficiente, \( \eta\). Então, é possível indagar se o aumento do número de parcelas é acompanhado pela diminuição, ou tenha o efeito de diminuir correspondentemente o valor absoluto de \( \eta\).
Se isto for assim, a expressão para cada um dos pesos em 75 ou 76 assume a forma de uma integral. Mas, uma integral é uma soma cujo número de parcelas é indefinidamente grande. O treino normal de um Perceptron é finito, tem um número finito de atualizações de peso, embora este número finito possa ser grande. Ou seja, o aprendizado padrão de um Perceptron é limitado à sessão de treino após a qual ele é posto a desempenhar a sua tarefa produtiva.
Uma tal forma integral não tem como ser vista dentro de um quadro de aprendizado já concluído ou com término definido. Ela pressupõe um número infinito de passos de treino, o que significa, concretamente, que o treino nunca terminaria, ou seja, aprendizado contínuo. A beleza disto, é que o aprendizado contínuo não afasta, de modo algum, o trabalho produtivo, mas revela a possibilidade de atualização e adequação do Perceptron a tarefas com características que se alterem com o tempo ou até mesmo adequação a tarefas completamente diferentes como é o caso em se tratando de aprendizado por transferência.
e
Se, como dissemos, quando \( t\rightarrow \infty\), temos \( \eta_t\rightarrow 0\), mas mantém-se não nulo, então, podemos avançar para a seguinte fórmula
onde fizemos \( \eta_{\tau+1}=d\tau\), pois se \( \eta\) for pequeno o suficiente, ele pode se considerado como a diferença entre dois instantes \( \tau+1\) e \( \tau\), de tempos bem próximos. Também, considerei \( W^l_1=W^l_{t_0}\), pois, como dissemos, o aprendizado contínuo compreende uma quantidade indeterminada de sessões de treino de prazo determinado. Então, cada sessão de treino culmina em um conjunto de pesos que passa a ser o \( W^l_{t_0}\) da próxima sessão.
Há alguns desenvolvimentos sugeridos na segunda equação de 106, mas nós não nos ocuparemo deles neste livro. Fica, no entanto, a forma dada nesta integral que assenta a possibilidade matemática para o aprendizado continuado cuja realização já se efetivou, haja vista a vantajosa técnica do aprendizado por transferência que é utilizada com tanto sucesso hoje em dia.
Apêndice G: A Função de Custo sobre um Domínio Matricial é uma Norma
Aqui, precisamos mostrar que o erro, \( E\), como definido em 86, é uma norma, de acordo com a definição dada em Norma Sobre Um Espaço Vetorial. A Função de Erro definida, aí, tem domínio matricial e está definida sobre uma outra norma, \( E_j\), que por sua vez tem domínio vetorial.
Proposição 1:
Se \( E_j\) é uma norma, então \( E=\frac{1}{\beta}\sum_{j=1}^{\beta}E_j(A^j)\) também o é.
Prova:
Precisamos mostrar que \( E\) atende aos 3 requisitos dados na Definição 1.
Como \( E_j\) é uma norma e \( \beta>0\), segue-se que se \( A^j\ne 0\),
Logo, \( E\) atende ao primeiro requisito da Definição Norma Sobre Um Espaço Vetorial.
O Erro \( E\) também atende ao segundo requisito pois, se \( a\in \mathbb{R}\), então,
Por fim, a desigualdade triangular também é satisfeita. Vejamos:
Apêndice H: Tópicos Fundamentais em Aprendizado de Redes Neurais Não Tratados Neste Livro
Perguntei ao ChatGPT quais seriam os tópicos mais importantes para a aprendizagem de máquinas, além da propagação para trás. A sua resposta está abaixo, com edições minhas.
Embora, você mesmo possa fazer a mesma pergunta a ele, coloquei-a aqui para que você possa acessar e ler prontamente o conteúdo da resposta.
Abaixo estão 9 tópicos essenciais para tornar o aprendizado de redes neurais possível ou para aprimorá-lo, além da já conhecida retropropagação (backpropagation).
H.1. Inicialização de Pesos
A maneira como os pesos da rede são inicializados pode impactar fortemente o sucesso do treinamento. Inicializações inadequadas podem levar ao desvanecimento (gradientes muito pequenos) ou à explosão (valores muito grandes) dos gradientes durante a retropropagação, dificultando ou impedindo o aprendizado. Inicializações modernas foram desenvolvidas para manter os valores das ativações e dos gradientes dentro de faixas estáveis, desde as primeiras até as últimas camadas.
Exemplos:
-
Inicialização de Xavier (Glorot) – ideal para funções de ativação simétricas como tanh.
-
Inicialização de He – recomendada para redes com ReLU.
H.2. Normalização de Dados
Normalizar os dados antes de inseri-los na rede é uma prática crítica para melhorar a convergência do treinamento. Dados com escalas muito distintas podem causar instabilidades ou tornar o treinamento lento. Além disso, normalizar as ativações internas das redes (durante o treinamento) ajuda a manter distribuições estáveis e acelera o aprendizado.
Exemplos:
-
Batch Normalization – normaliza as ativações em mini-lotes, além de introduzir dois parâmetros treináveis de escala e deslocamento.
-
Layer Normalization – usada em RNNs e Transformers, pois não depende do tamanho do lote.
H.3. Taxa de Aprendizado e Otimizadores
A taxa de aprendizado é o hiperparâmetro mais sensível de uma rede. Ela determina o tamanho dos passos dados no espaço de parâmetros a cada atualização. Se for muito alta, a rede pode nunca convergir; se for muito baixa, o treinamento pode ser lento ou ficar preso em mínimos locais. Otimizadores modernos melhoram esse processo adaptando automaticamente os passos com base nos gradientes acumulados ou momentos anteriores.
Exemplos:
-
SGD (Stochastic Gradient Descent) – versão básica, com ou sem momentum.
-
Adam – combina RMSprop com momentum; muito usado por sua robustez.
-
RMSprop – adapta a taxa de aprendizado dividindo os gradientes por uma média móvel dos quadrados dos gradientes passados.
H.4. Regularização
Regularização é o conjunto de técnicas que combatem o overfitting, que ocorre quando a rede memoriza os dados de treinamento e falha em generalizar para novos exemplos. Isso é especialmente importante em redes profundas, com grande capacidade de parametrização. A regularização impõe restrições sobre os pesos ou o comportamento da rede para favorecer modelos mais simples e robustos.
Exemplos:
-
L1 e L2 regularization – adicionam penalidades sobre o valor absoluto ou o quadrado dos pesos, respectivamente.
-
Dropout – desliga aleatoriamente unidades da rede durante o treinamento, forçando redundância e evitando coadaptação excessiva.
H.5. Arquiteturas de Rede
A arquitetura da rede determina sua capacidade expressiva e sua adequação à tarefa. A escolha da arquitetura afeta diretamente o desempenho, tempo de treinamento e interpretabilidade. Com o avanço das pesquisas, surgiram modelos especializados para diferentes tipos de dados (imagens, texto, som, séries temporais etc.), cada um aproveitando estruturas e propriedades específicas desses dados.
Exemplos:
-
Feedforward (MLP) – redes básicas com camadas densas (exatamente as que vimos neste livro, MLP ou Feedforward são apenas outros nomes).
-
CNNs (Convolutional Neural Networks) – exploram a estrutura espacial de imagens.
-
RNNs, LSTMs, GRUs – boas para dados sequenciais, como textos e sinais.
-
Transformers – arquitetura dominante para NLP e também aplicada em visão.
H.6. Engenharia de Dados e Pré-processamento
O desempenho de uma rede está diretamente relacionado à qualidade e representatividade dos dados que ela recebe. Dados ruidosos, incompletos ou enviesados podem comprometer todo o processo de aprendizado. Pré-processar e enriquecer os dados é um passo essencial, e muitas vezes mais importante do que ajustes finos nos hiperparâmetros.
Exemplos:
-
Limpeza de dados – remoção de duplicatas, tratamento de valores ausentes.
-
Aumento de dados (data augmentation) – criação de novas amostras artificiais, comum em visão computacional (ex: espelhamento, rotação).
-
Extração de características – como PCA ou t-SNE, para melhorar a representação dos dados.
H.7. Técnicas de Treinamento
O modo como a rede é treinada influencia fortemente sua capacidade de convergir para uma boa solução. Técnicas eficazes de treinamento ajudam a evitar problemas como ruído excessivo nas atualizações ou sobreajuste aos dados de treino. Algumas delas são estratégias para parar o treinamento no momento certo ou dividir os dados de forma que as atualizações sejam mais estáveis.
Exemplos:
-
Mini-batch training – divisão do conjunto de dados em pequenos blocos; equilibra precisão e velocidade.
-
Early stopping – monitora a performance em validação e interrompe o treino se esta piorar.
-
Learning rate schedules – reduzem a taxa de aprendizado ao longo do tempo para facilitar a convergência.
H.8. Curvas de Aprendizado e Avaliação
Acompanhar o comportamento da rede ao longo do tempo é crucial para diagnosticar problemas e guiar decisões. As curvas de perda e acurácia durante o treinamento e a validação revelam sinais de overfitting, underfitting ou erro de modelagem. Além disso, métricas apropriadas ajudam a avaliar corretamente a rede de acordo com o contexto do problema.
Exemplos:
-
Loss vs. Accuracy – duas curvas básicas a serem monitoradas.
-
F1-score, Precision, Recall – importantes em tarefas desequilibradas como detecção de fraude.
-
AUC-ROC – útil em classificadores binários para medir separabilidade.
H.9. Transferência de Aprendizado (Transfer Learning)
Embora haja um apêndice abordando alguns aspectos do Aprendizado por Transferência, aquele conteúdo está longe de cobrir o assunto e, em verdade, representa muito mais um ensaio feito por este autor. Transfer learning permite reaproveitar conhecimento de uma rede treinada em uma grande base de dados e adaptá-la a uma nova tarefa com menos dados. Isso é extremamente útil quando os dados disponíveis são escassos, mas a tarefa é semelhante a outra já bem explorada. Ele reduz o tempo de treinamento e melhora a generalização, sendo hoje uma prática comum, especialmente em NLP e visão computacional.
Exemplos:
-
Fine-tuning de redes como ResNet, BERT, GPT – adaptando os pesos finais a uma nova tarefa.
-
Congelamento de camadas – mantendo pesos já treinados e treinando apenas as camadas finais.
-
Uso de embeddings pré-treinados – como word2vec ou GloVe para texto.